4.6 Limites

Nous allons débuter en rappelant la définition de la limite d’une fonction à une variable.

Définition 4.5 (Limite d’une fonction à une variable) Soit une fonction \(f(x)\). Nous disons que \(L\) est la limite de \(f(x)\) lorsque \(x\) tend vers \(a\) si pour tout \(\epsilon >0\), il existe \(\delta\) tel que si \(|x-a|<\delta\) alors \(|f(x)-L|<\epsilon\). Nous notons alors: \[ \lim_{x\to a} f(x) = L \]

WIP

Proposition 4.1 (Les propriétés des limites) Soit \(f(x,y)\) et \(g(x,y)\) deux fonctions de deux variables.

\[\begin{align*} & \lim_{(x,y)\to(a,b)}f(x,y)\pm g(x,y)=\lim_{(x,y)\to(a,b)}f(x,y)\pm \lim_{(x,y)\to(a,b)} g(x,y) \\ & \lim_{(x,y)\to(a,b)}f(x,y)\cdot g(x,y)=\lim_{(x,y)\to(a,b)}f(x,y)\cdot \lim_{(x,y)\to(a,b)} g(x,y) \\ & \lim_{(x,y)\to(a,b)}\dfrac{f(x,y)}{g(x,y)}=\dfrac{\lim\limits_{(x,y)\to(a,b)}f(x,y)}{ \lim\limits_{(x,y)\to(a,b)} g(x,y)}\quad \text{si $g(x,y)\neq 0$ près de $(a,b)$} \end{align*}\]

Exemple 4.8 Trouvez la limite suivante:

\[ \lim_{(x,y)\to(1,2)} (x^2+y) \]

Exemple 4.9 Trouvez la limite suivante:

\[ \lim_{(x,y)\to(0,0)}\dfrac{\sin (x^2+y^2)}{x^2+y^2} \]

Nous avons pu lever l’indétermination de l’exemple 4.9 en utilisant une limite vue dans un cours de calcul intégral. Malheureusement, il sera habituellement plus difficile de lever des indéterminations. En particulier, il n’existe pas d’analogue à la règle de L’Hospital pour des fonctions de deux variables ou plus.

Nous verrons par contre deux techniques pour être en mesure de calculer des limites de fonctions de deux variables ou plus: la méthode des chemins et la méthode du gendarme.

4.6.1 La méthode des chemins

Cette méthode est une généralisation du principe de la limite à droite et de la limite à gauche. Lorsque nous avons:

\[ \lim_{x\to a} f(x) \]

cela signifie que la valeur de \(x\) s’approche de \(a\). La variable \(x\) peut s’approcher de \(a\) de deux façons différentes, par la droite ou par la gauche. Dans le cas de la limite suivante:

\[ \lim_{(x,y)\to (a,b)} f(x,y) \]

cela signifie que nous devons nous approcher du point \((a,b)\). Par contre, il existe plus de deux façons de se rendre au point \((a,b)\). Il en existe en fait une infinité! La figure 4.18 présente une représentation d’une limite pour une fonction d’une seule variable dans la figure de gauche. Dans la figure de droite, nous montrons trois chemins possibles, parmi l’infinité de chemins possibles.

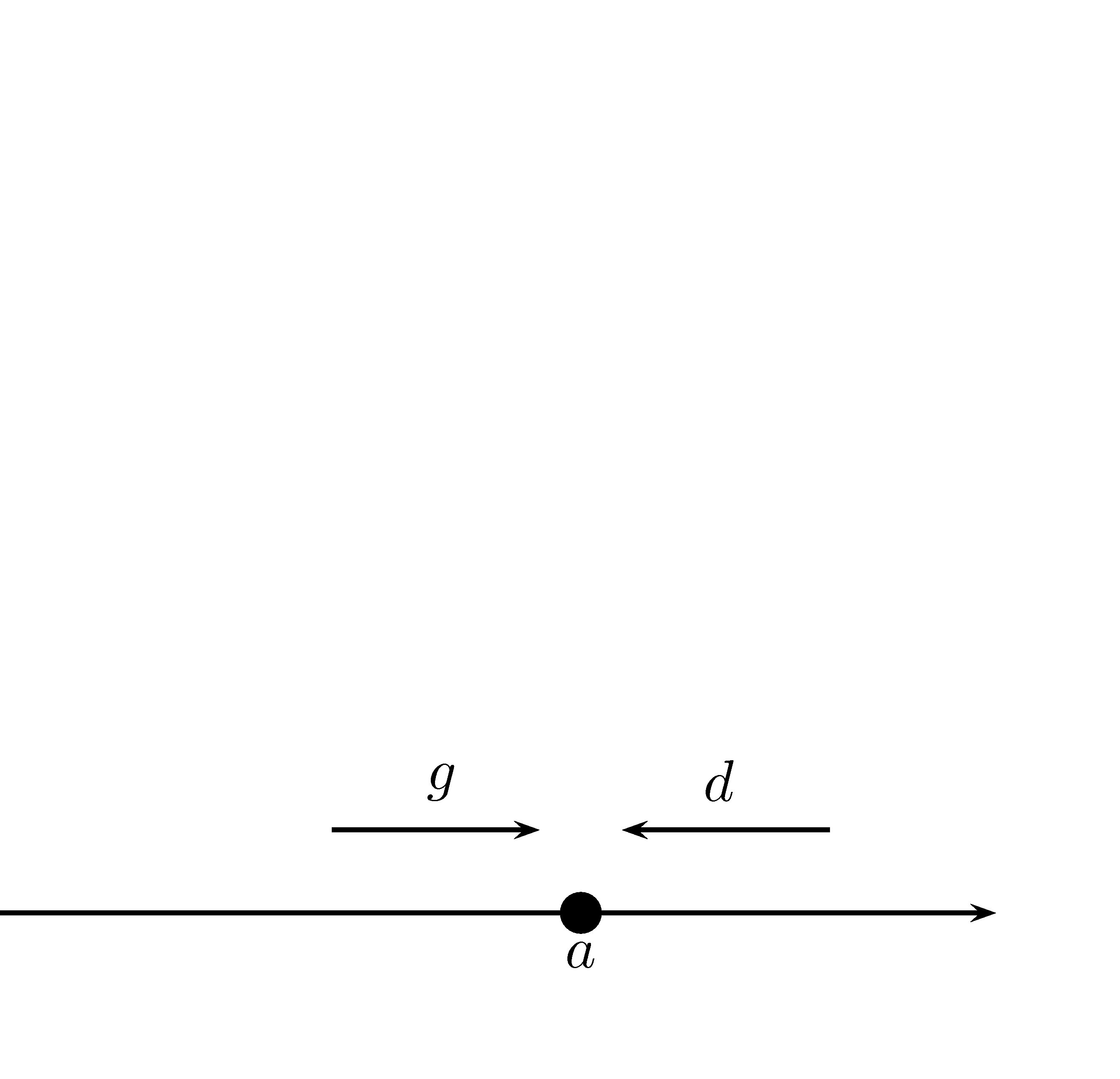
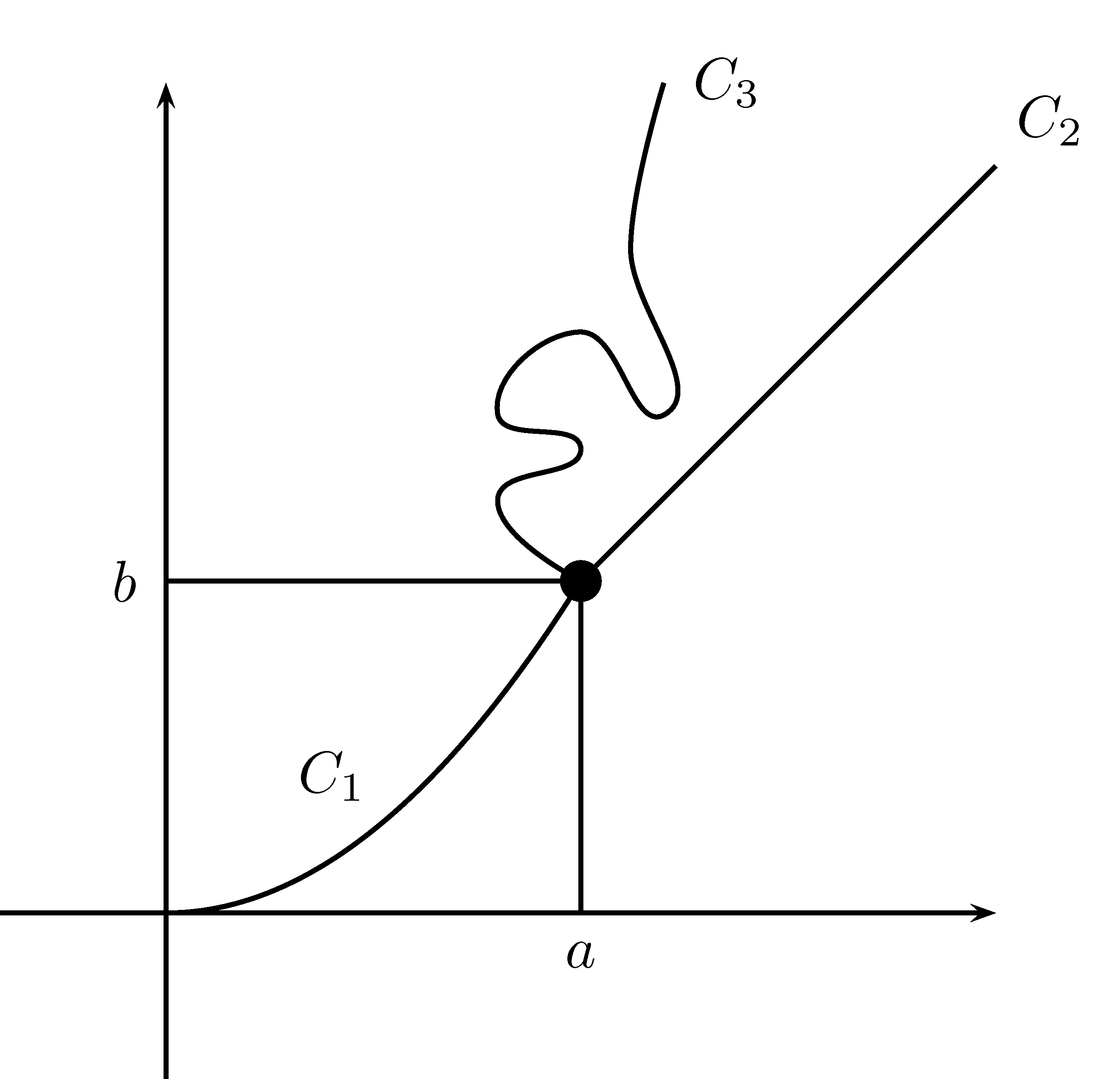
Figure 4.18: Représentation d’une limite en deux dimensions et d’une autre en trois dimensions.

Exemple 4.10 Déterminez, si elle existe, la limite suivante:

\[ \lim_{(x,y)\to (0,0)}\dfrac{x^2}{x^2+y^2} \]

En général, nous désirons trouver la limite en \((0,0)\) et nous allons tester les chemins suivants:

• \(x=0\)
• \(y=0\)
• \(y=x\)
• \(y=kx\) où \(k\) est une constante
• \(y=kx^2\) où \(k\) est une constante

Remarque. La méthode des chemins ne permet que de démontrer qu’une limite n’existe pas.

Exemple 4.11 Déterminez, si elle existe, la limite suivante:

\[ \lim_{(x,y)\to (0,0)}\dfrac{xy}{x^2+y^2} \]

Exemple 4.12 Déterminez, si elle existe, la limite suivante:

\[ \lim_{(x,y)\to (0,0)}\dfrac{xy^2}{x^2+y^4} \]

Exemple 4.13 Déterminez, si elle existe, la limite suivante:

\[ \lim_{(x,y)\to (0,0)}\dfrac{x^2+y^2}{y} \]

4.6.2 La méthode des gendarmes

Puisque la méthode des chemins ne nous permet pas de démontrer qu’une limite existe, nous allons introduire la méthode des gendarmes, qui elle permet de démontrer qu’une limite existe. Nous débutons pas utiliser la méthode des chemins pour calculer la limite:

\[ \lim_{(x,y)\to (a,b)}f(x,y) \]

Si tous les chemins nous donnent une limite égale à \(L\), nous pouvons présumer que:

\[ \lim_{(x,y)\to (a,b)}f(x,y)=L \]

Nous voulons maintenant trouver une fonction \(M(x,y)\) telle que:

\[ 0 \leq |f(x,y)-L| \leq M(x,y) \]

et telle que la limite suivante est vérifiée:

\[ \lim_{(x,y)\to (a,b)} M(x,y) = 0 \]

Nous nous retrouvons donc dans la situation suivante:

\[\begin{align*} 0 &\leq |f(x,y)-L| &\leq M(x,y) \\ \lim_{(x,y)\to (a,b)} 0 &\leq \lim_{(x,y)\to (a,b)}|f(x,y)-L| &\leq \lim_{(x,y)\to (a,b)}M(x,y) \\ 0 &\leq \lim_{(x,y)\to (a,b)}|f(x,y)-L| &\leq 0 \end{align*}\]

Nous pouvons donc conclure que:

\[ \lim_{(x,y)\to (a,b)}f(x,y)=L \]

Pour utiliser la méthode des gendarmes, nous utiliserons à plusieurs reprises l’inégalité suivante.

Proposition 4.2 Soit \(x\) et \(y\) deux nombres réels. Nous avons: \[\begin{align*} \left|\dfrac{x^2}{x^2+y^2}\right| &\leq 1 \\ \left|\dfrac{y^2}{x^2+y^2}\right| &\leq 1 \end{align*}\]

Preuve. Nous avons: \[\begin{align*} x^2 &\leq x^2+y^2 \\ \dfrac{x^2}{x^2+y^2} &\leq 1 \end{align*}\] L’autre inégalité se démontre de la même manière.

Exemple 4.14 Trouvez la limite suivante: \[ \lim_{(x,y)\to (0,0)}\dfrac{x^2y}{x^2+y^2} \]

Exemple 4.15 Trouvez la limite suivante: \[ \lim_{(x,y)\to (0,0)}\dfrac{y^3}{x^2+y^2} \]

4.6.3 Exercises divers de limites

Exemple 4.16 Trouvez, si possible, les limites suivantes:

1. \(\lim_{(x,y)\to (2,-1)} (xy+y^2)\)
2. \(\lim_{(x,y)\to (0,0)} \sqrt{x^2+y^2}\)
3. \(\lim_{(x,y)\to (0,0)} \dfrac{x}{x^2+y^2}\)
4. \(\lim_{(x,y)\to (0,0)} \dfrac{\cos(xy)}{1-x-\cos(y)}\)
5. \(\lim_{(x,y)\to (0,1)} \dfrac{x^2(y-1)^2}{x^2+(y-1)^2}\)
6. \(\lim_{(x,y)\to (0,0)} \dfrac{\sin(x-y)}{\cos(x+y)}\)
7. \(\lim_{(x,y)\to (0,0)} \dfrac{\sin(xy)}{x^2+y^2}\)