2.2 Les équations différentielles à variables séparables

Définition 2.6 (Équation différentielle à variables séparables) Une équation différentielle à variables séparables est une équation différentielle qui peut s’écrire sous la forme \(M(y)dy=N(x)dx\).

Pour trouver la solution d’une équation différentielle à variables séparables, il faut:

• Mettre l’équation sous la forme différentielle, c’est-à-dire placer les différentielles au numérateur.
• Séparer les variables en se basant sur les différentielles.
• Intégrer de chaque côté de l’égalité, c’est-à-dire \(\int M(y)dy=\int N(x)dx\)

Exemple 2.5 Résolvez l’équation différentielle suivante: \(\cos(y)\dfrac{dy}{dt}=t^2\).

Remarque. Lorsque vous trouvez la solution d’une équation différentielle, il n’est pas toujours possible d’obtenir une équation explicite (c’est-à-dire une équation où la variable dépendante est isolée).

Exemple 2.6 Trouvez la solution de l’équation différentielle \(x+yy'=0\) passant par le point \((3,0)\).

Exemple 2.7 (Modèle de Hill-Keller) Le modèle de Hill-Keller permet de modéliser la course d’un coureur pour de courtes distances, par exemple le 100 m ou le 200 m. Si \(F\) est une constante qui correspond à la force du coureur et \(\tau\) est une constante représentant les forces de frottement du coureur, l’équation du modèle est donnée par: \(\dfrac{dv}{dt}=F-\dfrac{v}{\tau}\). Trouvez la vitesse d’un coureur en fonction du temps si au temps initial la vitesse du coureur est nulle.

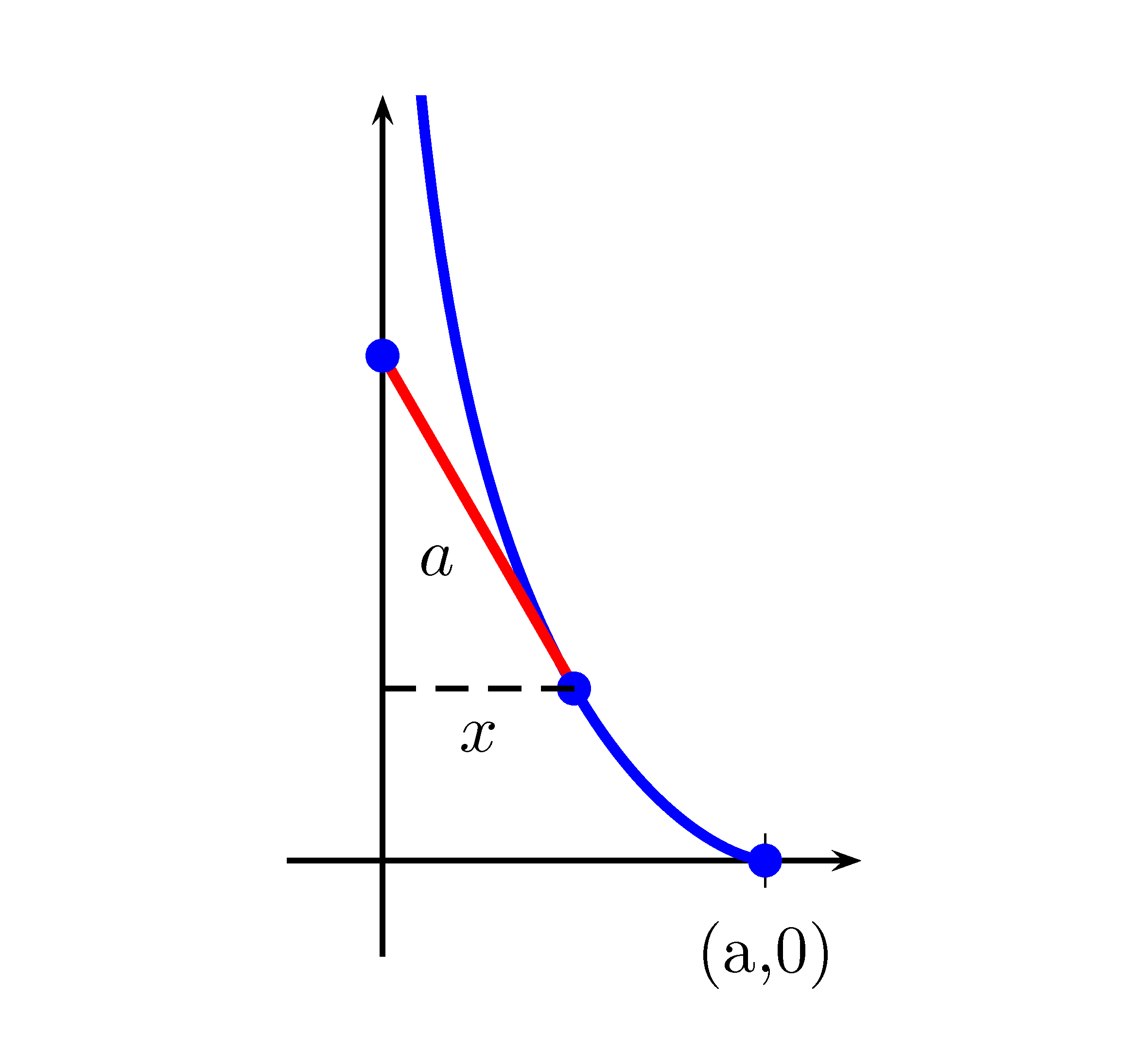
Exemple 2.8 (La tractrice) Vous avez une laisse rigide de longueur \(a\). Vous vous trouvez au point \((0,0)\) et votre chien se trouve au point \((a,0)\). Vous vous dirigez dans la direction de l’axe des \(y\) positifs. L’équation différentielle qui permet de trouver le parcours de votre chien est \(\dfrac{dy}{dx}=-\dfrac{\sqrt{a^2-x^2}}{x}\). Trouvez la solution de l’équation différentielle précédente.

Exemple 2.9 Trouvez les trajectoires orthogonales de la famille \(x=ky^2\).

Exemple 2.10 Trouvez les trajectoires orthogonales de la famille \(y=ke^x\).

Exemple 2.11 Soit un parachutiste qui tombe sous l’effet de la gravité avec une résistance de l’air proportionnelle à sa vitesse. L’équation différentielle de cette situation est : \(\dfrac{dv}{dt}+\dfrac{kv}{m}=g\) où \(m\), \(g\) et \(k\) sont des constantes positives. Trouvez la solution de l’équation différentielle précédente.

Exemple 2.12 La loi de refroidissement de Newton dit que le taux de variation de la température \(T\) d’un objet est proportionnel à la différence entre la température de cet objet et la température ambiante (notée \(T_A\)). Trouvez l’équation différentielle décrivant le phénomène et trouvez \(T\) en fonction du temps.