Calcul différentiel et intégral dans l’espace

3.1 Introduction

Les coordonnées polaires sont un autre système pour décrire un point $P$ de $\mathbb{R}^2$. Les coordonnées cartésiennes associent à chaque point $P$ un couple $(x,y)$. Les coordonnées polaires consistent à décrire ce point $P$ avec le couple $(r,\theta)$, où $r$ est la longueur du segment de droite reliant l’origine au point $P$ et $\theta$ est l’angle entre ce segment de droite et l’axe des $x$ positifs. La figure 3.1 représente ce type de coordonnées.

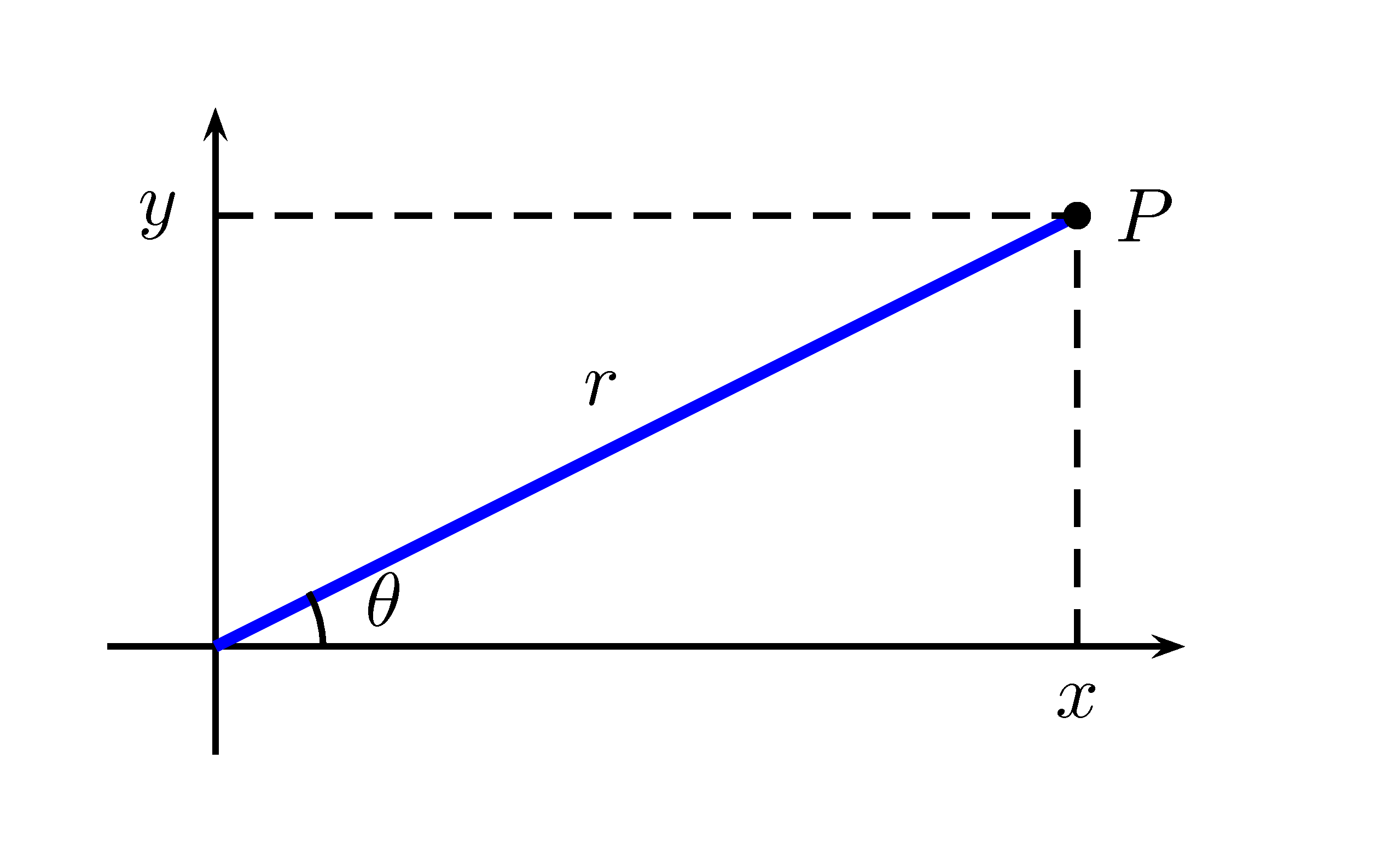
$Coordonnées polaires d'un point $P$$

Figure 3.1: Coordonnées polaires d’un point $P$

Il est primordial de pouvoir convertir les coordonnées cartésiennes à des coordonnées polaires et vice-versa.

Proposition 3.1 (Coordonnées cartésiennes à coordonnées polaires) Soit un point $P$ en coordonnées cartésiennes $(x,y)$. La conversion en coordonnées polaires est: \[\begin{align*} r &= \sqrt{x^2+y^2} \\ \theta &= \text{Arctan}\left(\dfrac{y}{x}\right) \end{align*}\]

Proposition 3.2 (Coordonnées polaires à coordonnées cartésiennes) Soit un point $P$ en coordonnées polaires $(r,\theta)$. La conversion en coordonnées cartésiennes est: \[\begin{align*} x &= r\cos(\theta) \\ y &= r\sin(\theta) \end{align*}\]

Remarque. Voici quelques remarques:

L’origine, c’est-à-dire le point $(0,0)$ en coordonnées cartésiennes, que l’on appelle pôle, peut s’écrire $(0,\theta)$, et ce, pour toutes les valeurs de $\theta$ possibles. Ceci signifie qu’il n’existe pas de bijection¹ entre les coordonnées cartésiennes et polaires. Par contre, si on enlève l’origine, il en existe une.
Lorsque l’on fixe $\theta=\theta_0$, l’ensemble formé par $(r,\theta_0)$est une demi-droite. En acceptant que $r$ soit négatif, on obtient alors que $(r,\theta_0)$ forme une droite.
Si $r>0$, alors $(-r,\theta_0)=(r,\theta_0+\pi)$.

Exemple 3.1 Écrivez les points suivants en coordonnées polaires:

$P_1=(1,1)$
$P_2=(-\sqrt{3},1)$
$P_3=(0,-2)$

Exemple 3.2 Écrivez les points suivants en coordonnées cartésiennes:

$(2,\pi/3)$
$(3,3\pi/4)$

Exemple 3.3 Écrivez l’équation de la perle de Sluze en coordonnées polaires, si $y^2=x(8-x)$.

Une bijection est une fonction $f$ allant d’un ensemble $A$ à un ensemble $B$, telle que pour tous les éléments de $B$, on associe une seule valeur de $A$.↩