8.4 Intégrales triples en coordonnées sphériques
Nous allons débuter en introduisant les coordonnées sphériques.
Définition 8.2 (Coordonnées sphériques) Soit un point \((x,y,z)\in\mathbb{R}^3\) en coordonnées cartésiennes. Nous pouvons représenter ce point en coordonnées cylindriques en effectuant les transformations suivantes:
\[\begin{align*}
x &= \rho\cos(\theta)sin(\phi) \\
y &= \rho\sin(\theta)sin(\phi) \\
z &= \rho\cos(\phi)
\end{align*}\]
avec les conditions suivantes:
\[\begin{align*}
0 \leq \rho \leq \infty \\
0 \leq \theta \leq 2\pi \\
0\leq \phi \leq \pi
\end{align*}\]
Nous avons que \(\rho\) représente la longueur du segment de droite reliant l’origine au point \(P\), \(\theta\) est l’angle que fait la projection du segment de droite sur le plan \(z=0\) et \(\phi\) est l’angle que fait le segment de droite par rapport à l’axe des \(z\).
La figure 8.2 représente un point en coordonnées cylindriques.
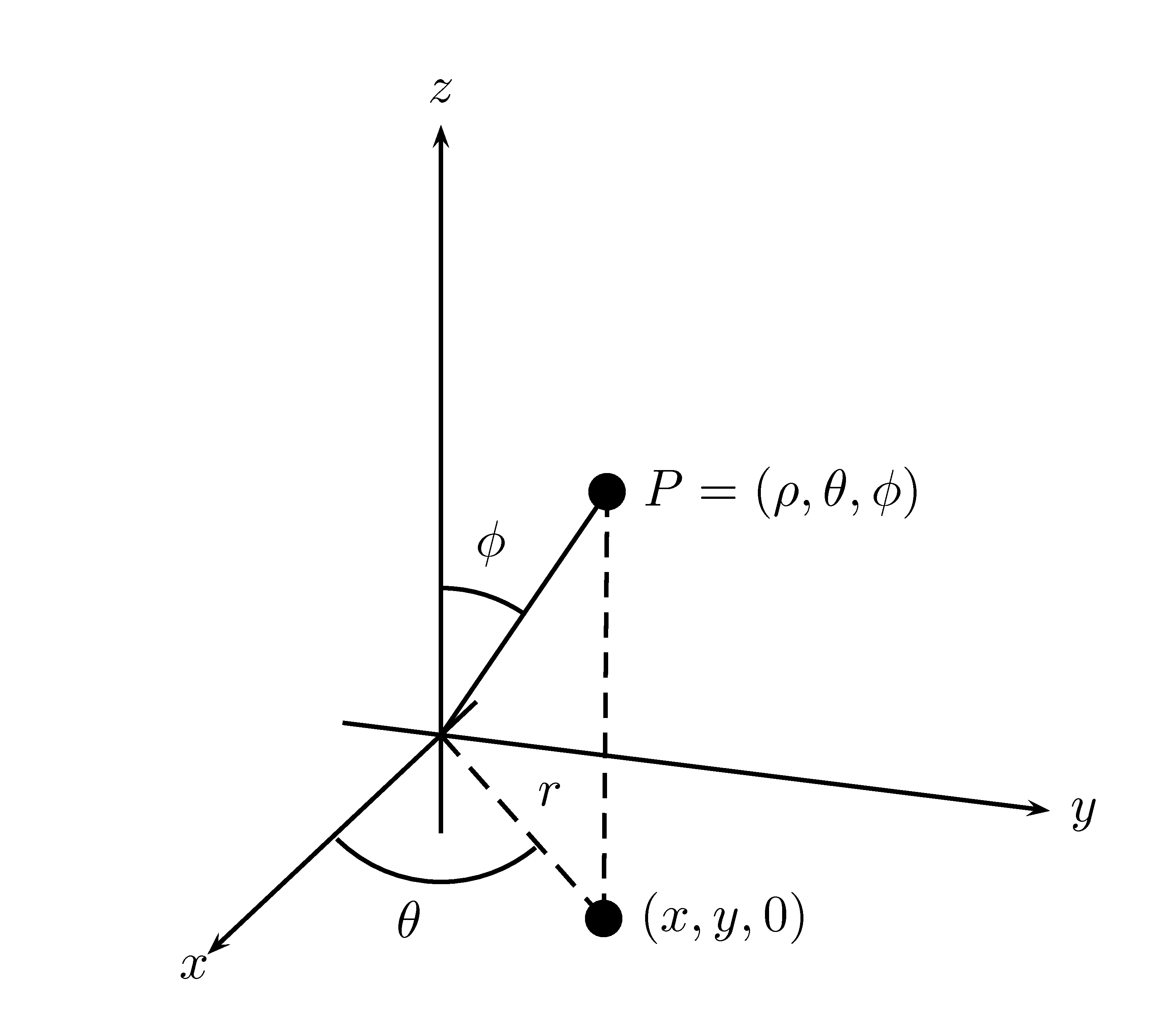
Figure 8.2: Un point \(P\) représenté en coordonnées sphériques.
Exemple 8.12 Calculez le volume d’une sphère de rayon \(a\).
Exemple 8.13 Calculez le volume à l’intérieur du cône \(z=\sqrt{x^2+y^2}\) et de la sphère \(x^2+y^2+z^2=a^2\).