5.2 Les dérivées partielles
Nous allons débuter en rappelant la définition de la dérivée d’une fonction d’une seule variable.
Nous savons que la dérivée d’une fonction correspond, entre autres, à la pente de la droite tangente. Dans le cas d’une fonction de plus d’une variable, la notion de pente de droite tangente en un point n’existe pas à priori. Nous devrons donc définir une nouvelle définition de dérivée.
Nous allons débuter par introduire la notion de dérivée pour les fonctions de deux variables. La généralisation pour les fonctions de plus de deux variables se fait facilement.
Soit une fonction \(z=f(x,y)\). Pour étudier les deux (une par variable indépendante) dérivées partielles de cette fonction, nous allons les variations de cette fonction.
Supposons que nous nous trouvons dans un plan où la variable \(y\) est constante. Ceci signifie que seule la variable \(x\) varie, c’est-à-dire que nous partons du point \((x,y)\) jusqu’au point \((x+\Delta x,y)\). Puisque nous avons deux points, nous pouvons déterminer le taux de variation de la fonction \(f(x,y)\) par rapport à la vraible \(x\). Ce taux est donné par:
\[ \dfrac{f(x+\Delta x,y)-f(x,y)}{\Delta x} \]
Lorsque nous prenons la limite de ce taux de variation lorsque \(\Delta x\) tend vers \(0\), nous obtenons la dérivée partielle de \(f(x,y)\) par rapport à \(x\). Mathématiquement, nous écrivons:
\[ \dfrac{\partial f}{\partial x}=\lim_{\Delta x \to 0} \dfrac{f(x+\Delta x,y)-f(x,y)}{\Delta x} \]
D’une manière similaire, nous pouvons définir la dérivée partielle de \(f(x,y)\) par rapport à \(y\):
\[ \dfrac{\partial f}{\partial y}=\lim_{\Delta y \to 0} \dfrac{f(x,y+\Delta y)-f(x,y)}{\Delta y} \]
Géométriquement, la dérivée partielle de \(f(x,y)\) par rapport à \(x\) correspond à la pente de la droite tangente à la courbe engendrée par l’intersection du plan \(y=k\) où \(k\) est une constante et la surface \(z=f(x,y)\).
La figure 5.1 représente dans l’image de gauche la surface \(z=f(x,y)\) coupée par le plan \(y=k\) où \(k\) est une constante. Nous apercevons l’intersection de la surface et du plan, représentée par une courbe parabolique. La ligne pointillée représente la droite tangente à la surface dans le plan \(y=k\). La figure de droite représente la fonction parabolique dans le plan \(y=k\) ainsi que la droite tangente.

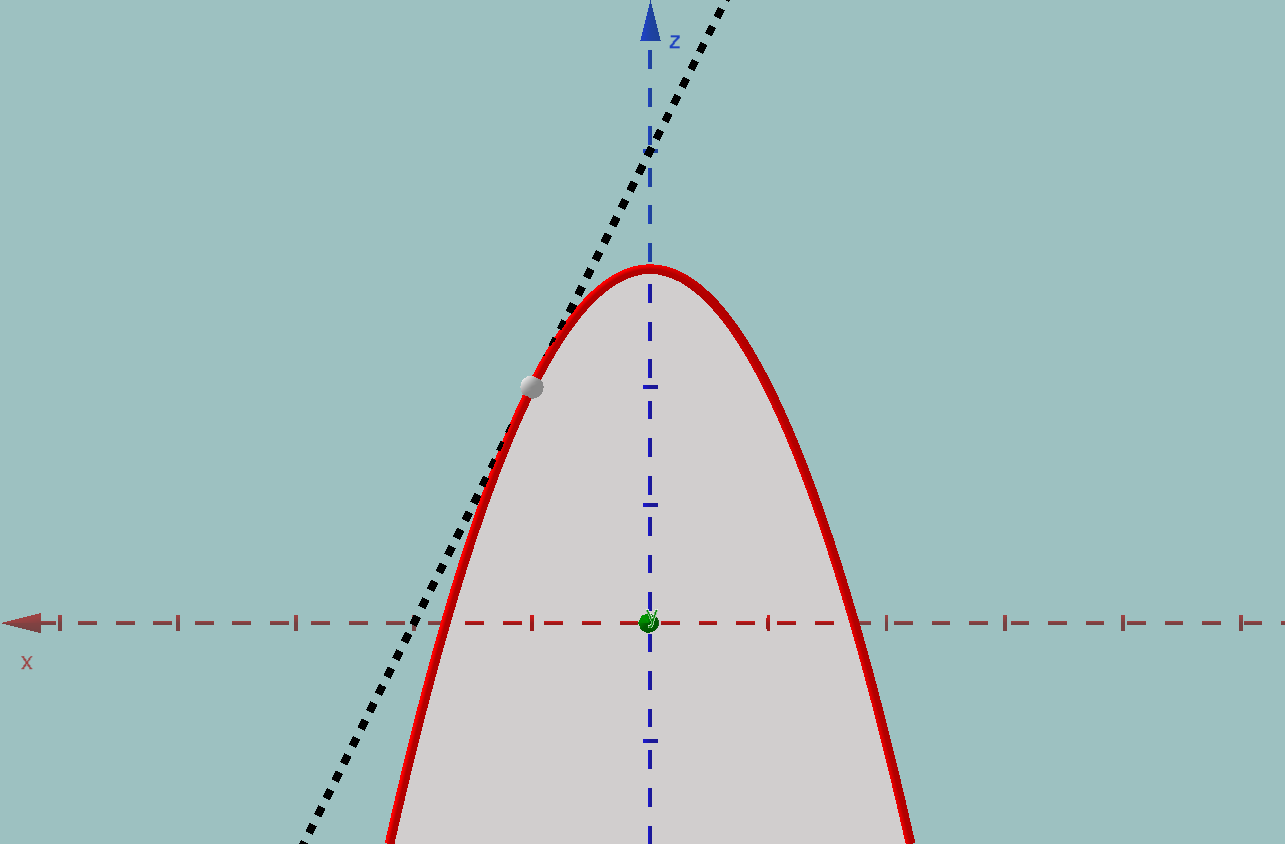
Figure 5.1: Représentation géométrique de la dérivée partielle de \(f(x,y)\) par rapport à \(x\)
C’est la même correspondance pour \(\dfrac{\partial f}{\partial y}\), il suffit d’étudier la courbe dans le plan \(x=k\) où \(k\) est une constante.
Lorsque nous trouvons la dérivée partielle d’une fonction \(f(x_1,x_2,\ldots,x_n)\) par rapport à la variable indépendante \(x_i\), nous supposons toutes les autres variables indépendantes \(x_j\) où \(j\neq i\) sont des constantes.
Proposition 5.1 (Notation pour dérivées partielles) Soit une fonction \(f(x_1,x_2,\ldots,x_n)\). La dérivée partielle de \(f\) par rapport à la variable \(x_i\) peut être notée par:
- \(f_{x_i}\)
- \(f_i\)
- \(\dfrac{\partial f}{\partial x_i}\)
- \(D_i f\)
Dans le cas où la fonction ne possède que deux variable, c’est-à-dire une fonction \(f(x,y)\), nous pouvons noter la dérivée partielle de \(f\) par rapport à \(x\) par:
- \(f_{x}\)
- \(\dfrac{\partial f}{\partial x}\)
- \(D_x f\)
Exemple 5.5 Soit une fonction \(f\) différentiable et d’une seule variable. Montrez que \(f\left(\frac{x}{y}\right)\) satisfait l’équation: \[ x\dfrac{\partial f}{\partial x}+y\dfrac{\partial f}{\partial y} = 0 \]
5.2.1 Les dérivées d’ordres supérieurs
Nous allons maintenant définir les dérivées d’ordres supérieurs. Voici les dérivées partielles secondes d’une fonction \(f(x,y)\).
Définition 5.2 (Les dérivées partielles du second ordre) Nous avons: \[\begin{align*} \dfrac{\partial^2 f}{\partial x^2} &= \dfrac{\partial}{\partial x}\left[\dfrac{\partial f}{\partial x}\right] = f_{xx}(x,y) = f_{11}(x,y) \\ \dfrac{\partial^2 f}{\partial y^2} &= \dfrac{\partial}{\partial y}\left[\dfrac{\partial f}{\partial y}\right] = f_{yy}(x,y) = f_{22}(x,y) \\ \dfrac{\partial^2 f}{\partial x \partial y} &= \dfrac{\partial}{\partial x}\left[\dfrac{\partial f}{\partial y}\right] = f_{yx}(x,y) = f_{21}(x,y) \\ \dfrac{\partial^2 f}{\partial y \partial x} &= \dfrac{\partial}{\partial y}\left[\dfrac{\partial f}{\partial x}\right] = f_{xy}(x,y) = f_{12}(x,y) \end{align*}\]
Théorème 5.1 (Le théorème de Clairaut) Soit une fonction \(f(x,y)\) définie sur un disque \(D\) qui contient le point \((a,b)\). Si \(f_{xy}\) et \(f_{yx}\) sont continues sur \(D\), alors: \[\begin{align*} f_{xy}(a,b)=f_{yx}(a,b) \end{align*}\]