3.4 Aire d’une région
Nous voulons maintenant trouver une formule afin de calculer l’aire d’une région formée par une courbe définie par \(r=f(\theta)\) avec \(\theta_a\leq \theta \leq \theta_b\).
Rappelons que l’aire \(A\) d’un secteur de cercle de rayon \(r\) est donnée par \(A=\dfrac{1}{2}r^2\theta\).
La figure 3.3 représente la surface que nous désirons trouver.
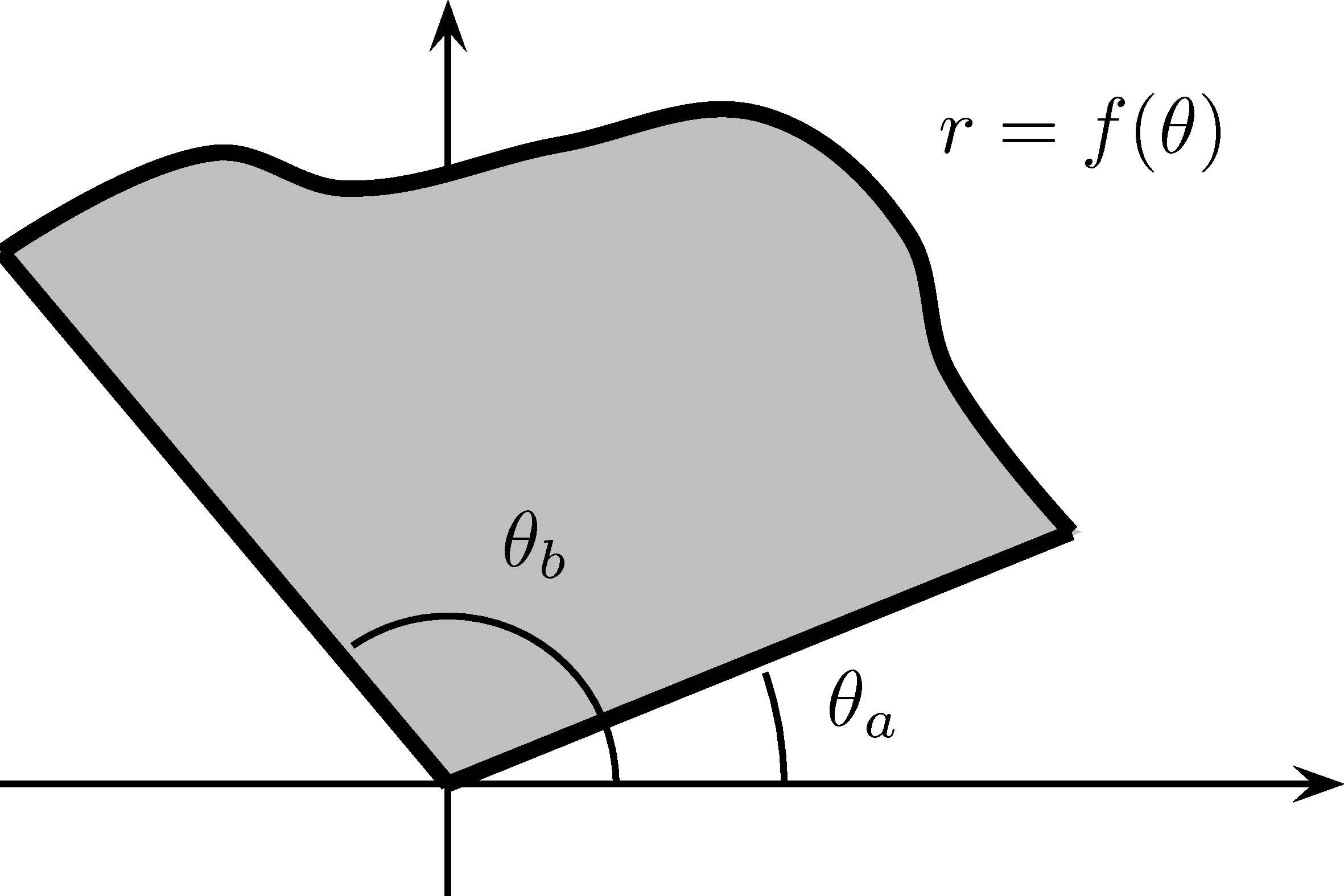
Figure 3.3: Aire d’une courbe polaire
Divisons l’intervalle \(\theta_a\leq \theta \leq \theta_b\) en \(N\) partitions de longueur \(\Delta \theta_i=\theta_i-\theta_{i-1}\) pour \(i=1,\ldots,N\). L’ensemble \[\begin{align*} \{\theta_0=\theta_a,\theta_1,...,\theta_{N-1},\theta_{N}=\theta_b\} \end{align*}\] est appelée partition de \(\theta_a\leq \theta \leq \theta_b\). L’aire de chacun de ces secteurs peut être approchée par: \[\begin{align*} A_i\approx \dfrac{1}{2}[f(\theta_i^*)]^2\Delta \theta_i, \quad \text{où $\theta_i^*\in [\theta_{i-1},\theta_{i}]$} \end{align*}\]
La figure 3.4 représente une partition.
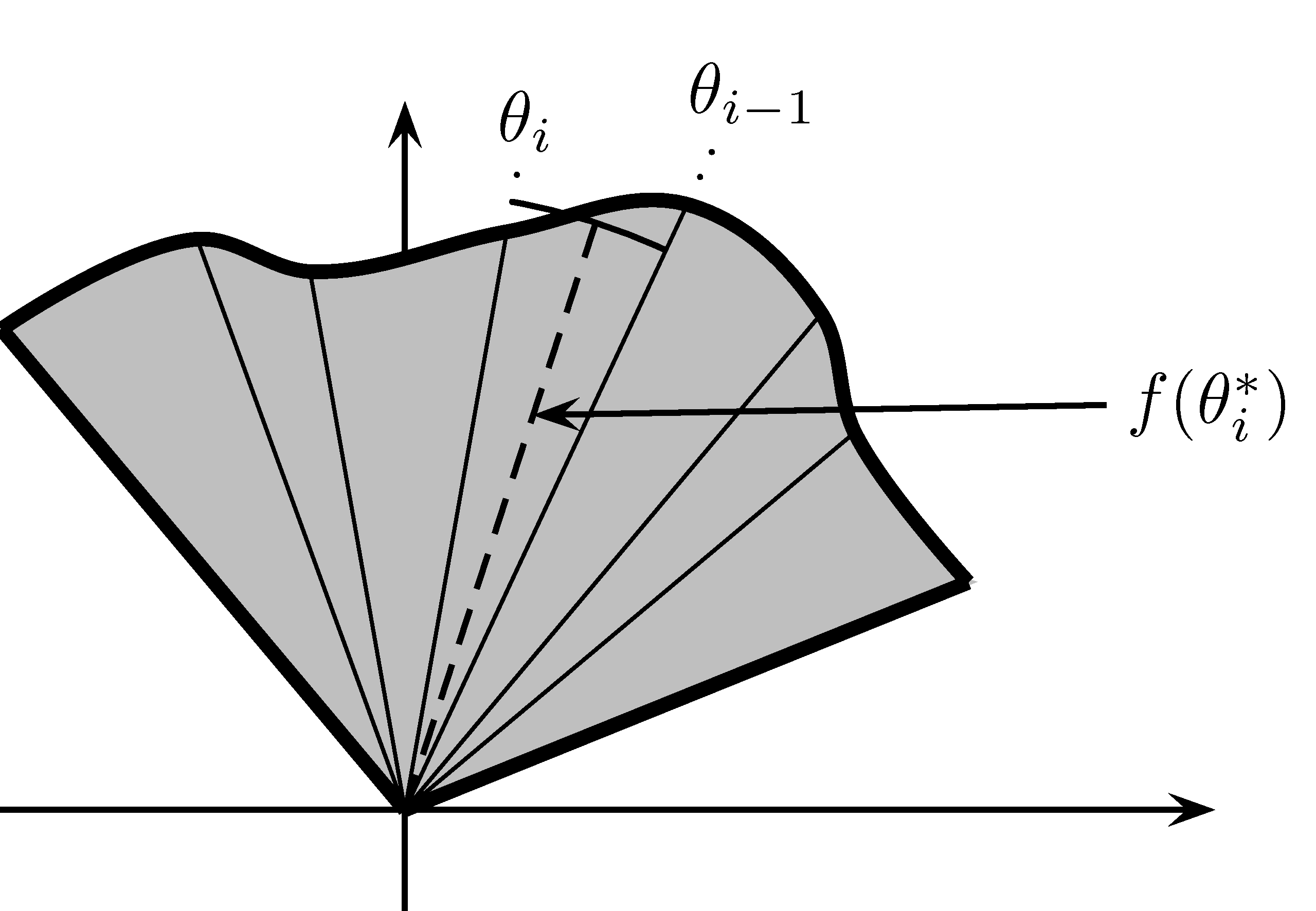
Figure 3.4: Aire d’une courbe polaire: séparation en secteurs
Nous voulons trouver l’aire totale, c’est-à-dire la somme des surfaces des \(N\) secteurs: \[\begin{align*} A\approx \sum_{i=1}^N\dfrac{1}{2}[f(\theta_i^*)]^2\Delta \theta_i \end{align*}\] Nous remarquons que cette somme est une somme de Riemann. Ainsi, en prenant la limite lorsque \(N\) tend vers l’infini, nous obtenons: \[\begin{align*} A=\lim_{N\rightarrow \infty } \sum_{i=1}^N\dfrac{1}{2}[f(\theta_i^*)]^2\Delta \theta_i=\int_{\theta_a}^{\theta_b}\dfrac{1}{2}[f(\theta)]^2d \theta \end{align*}\]
D’où, l’aire est donnée par: \[\begin{align*} A &= \int_{\theta_a}^{\theta_b}\dfrac{1}{2}[f(\theta)]^2 d\theta \end{align*}\]