4.2 Définitions

Débutons en rappelant le concept de fonction et en le généralisant aux fonctions de deux variables ou plus.

Définition 4.1 (Fonction) Soit un ensemble \(A\) et un ensemble \(B\). Une fonction \(f\) est une application qui pour chaque élément \(x\in A\) lui associe un seul élément \(y\in B\). On note cette fonction \[\begin{align*} f:\ A&\longrightarrow B\\ x&\longrightarrow y=f(x) \end{align*}\]

• L’ensemble \(A\) se nomme de \(f\), noté \(\text{dom}(f)\).
• L’ensemble \(B\) est le de la fonction \(f\), noté \(\text{codom}(f)\).

Définition 4.2 (Image d’une fonction) L’image d’une fonction est l’ensemble de tous les éléments du codomaine qui sont obtenus par la fonction \(f\). Nous notons l’image \(\text{ima}(f)\). En langage mathématique, l’image s’écrit comme suit: \[\begin{align*} \text{ima}(f):=\{y|y=f(x),\forall x\in dom(f)\} \end{align*}\] Il est à remarquer que \(\text{ima}(f)\subseteq \text{codom}(f)\).

La distinction entre l’image et le codomaine est représentée à la figure 4.1. Le codomaine est l’ensemble \(B\) tandis que l’image est l’ensemble de tous les éléments de \(B\) qui sont reliés à un ou plusieurs éléments de \(A\) par la fonction (ici l’image est la région ombragée).

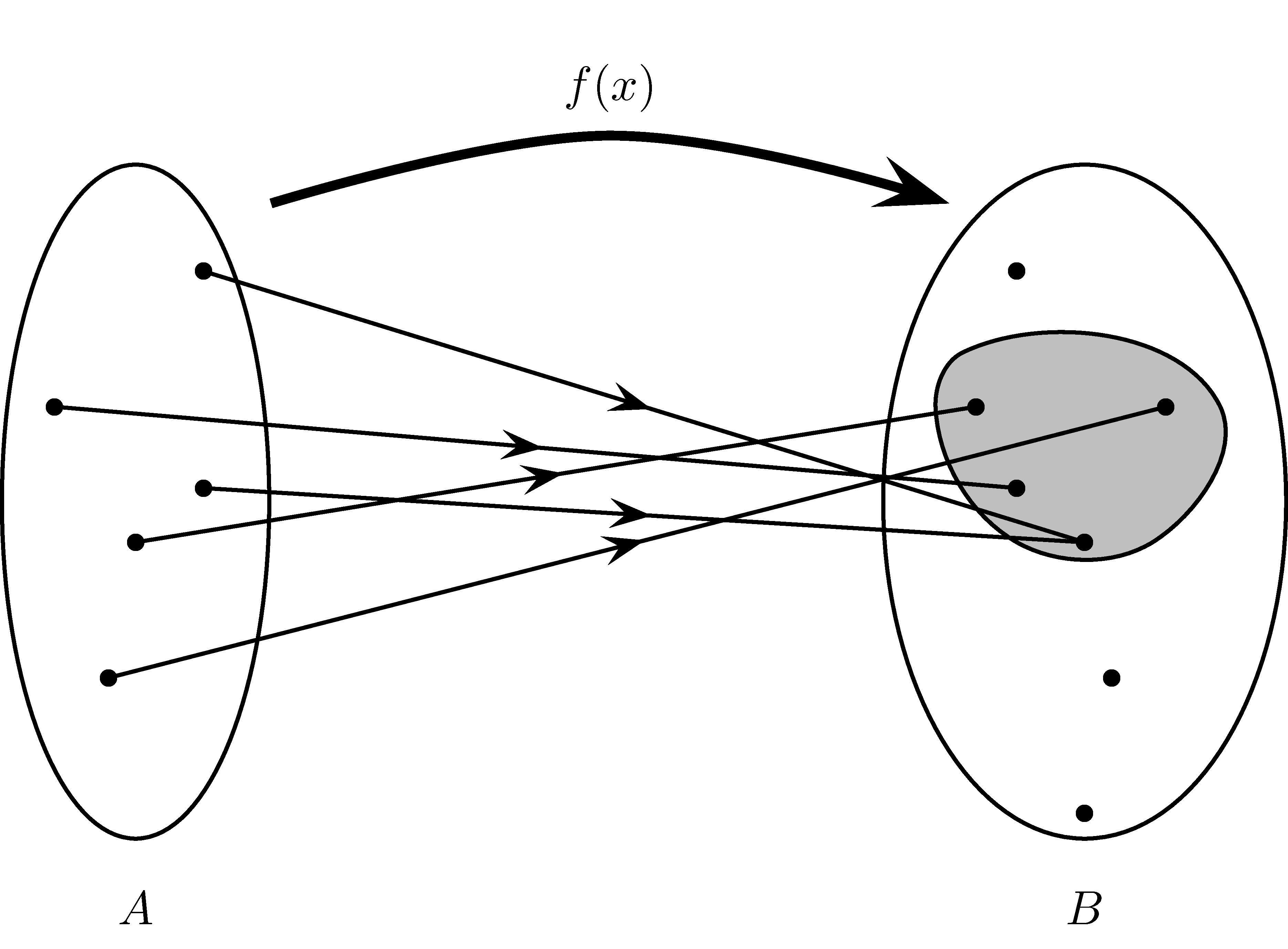
Figure 4.1: Graphique saggital représentant une fonction.

Jusqu’à maintenant, nous avons étudié les fonctions ayant comme domaine un sous-ensemble de la droite des réels. Dans ce cours, nous étudierons des fonctions ayant comme domaine un sous-ensemble \(\mathbb{R}^n\), où \(n\in\mathbb{N}\). En langage mathématique, ces fonctions s’écrivent: \[\begin{align*} f: D\subseteq \mathbb{R}^n &\longrightarrow \mathbb{R}\\ (x_1,..,x_n)&\longrightarrow z=f(x_1,..,x_n) \end{align*}\] où \(x_1\), …, \(x_n\) sont \(n\) variables indépendantes.