5.4 Le plan tangent

Nous désirons trouver l’équation du plan tangent à une surface donnée par la fonction \(z=f(x,y)\) au point \((x_0,y_0,z_0)\) où \(z_0=f(x_0,y_0)\). Pour ce faire, nous allons débuter en rappelant comment trouver l’équation cartésienne d’un plan.

5.4.1 L’équation cartésienne d’un plan

Définition 5.3 (Le vecteur normal à un plan) Soit un plan \(\pi\). Un vecteur normal au plan, noté \(\overrightarrow{n}\), est un vecteur tel que tous les vecteurs se trouvant sur le plan sont perpendiculaires à \(\overrightarrow{n}\).

Nous allons maintenant utiliser le vecteur normal au plan pour définir l’équation normale du plan de l’espace. Soit un plan \(\pi\) et un vecteur \(\overrightarrow{n}=[a,b,c]\) normal à ce plan. Soit aussi un point \(P(x_0,y_0,z_0)\) connu faisant partie du plan et un point \(Q(x,y,z)\) un point quelconque du plan. La figure 5.2 représente un plan ainsi que l’un de se vecteur normal avec un point \(P\) connu.

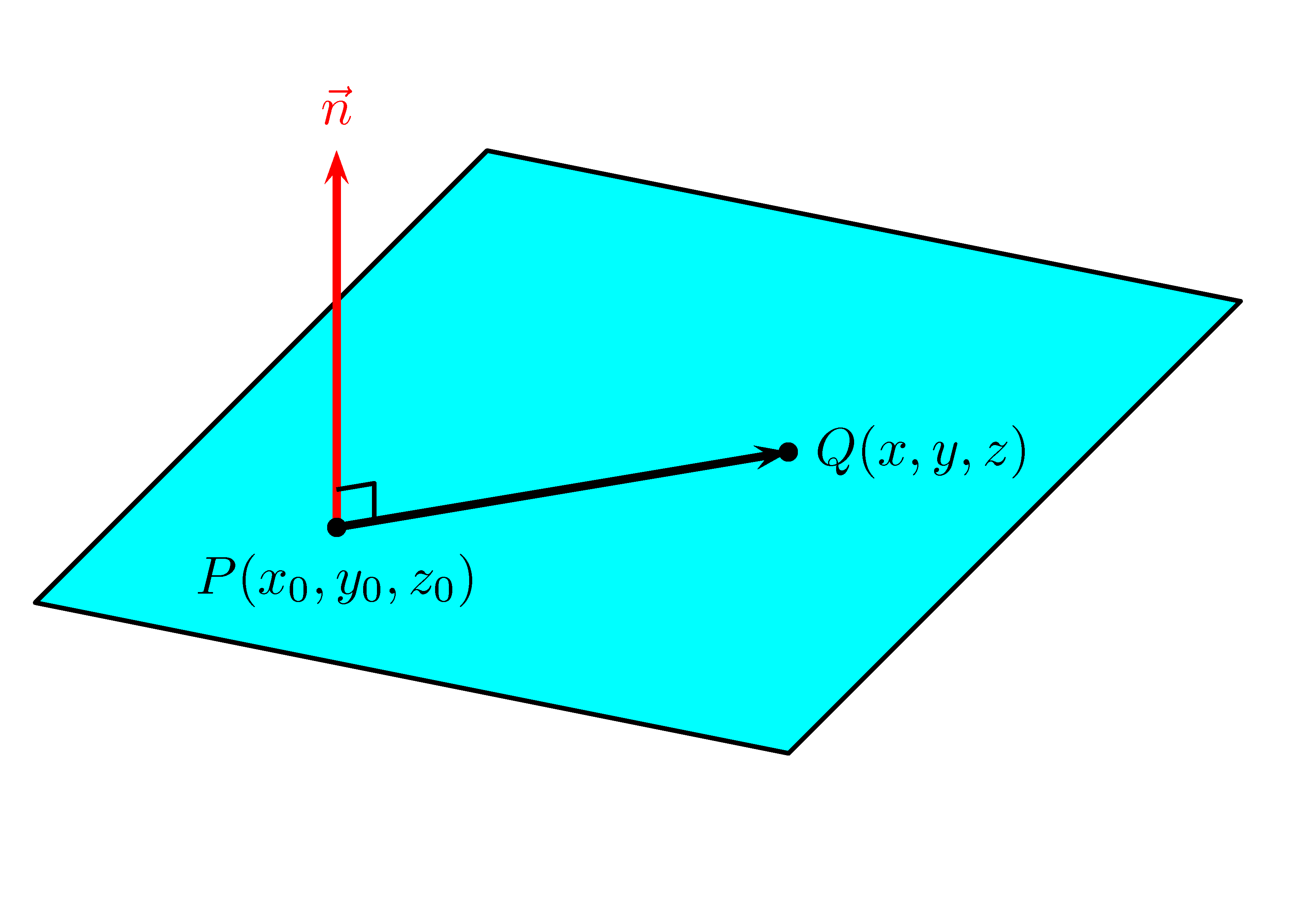
Figure 5.2: Représentation d’un plan avec un de ses vecteur normal.

Puisque le vecteur normal \(\overrightarrow{n}\) est perpendiculaire à tous les vecteurs se trouvant sur le plan, il est en particulier perpendiculaire au vecteur \(\overrightarrow{PQ}\). Si nous définissons le vecteur \(\overrightarrow{p} = \overrightarrow{OP}\) et le vecteur \(\overrightarrow{x}=\overrightarrow{OQ}\), nous avons que: \[\begin{align*} \overrightarrow{n} \cdot (\overrightarrow{x} - \overrightarrow{p}) &= 0 \quad \text{car $\overrightarrow{n} \perp (\overrightarrow{x} - \overrightarrow{p})$} \end{align*}\] Nous avons donc:

Définition 5.4 (L’équation cartésienne d’un plan) Soit un plan \(\pi\). Soit un vecteur normal à ce plan \(\overrightarrow{n}=[a,b,c]\) et un point de ce plan \(P(x_0,y_0,z_0)\) connu. L’équation normale du plan est donnée par: \[\begin{align*} \overrightarrow{n} \cdot (\overrightarrow{x} - \overrightarrow{p}) &= 0 \\ [a,b,c] \cdot [x-x_0,y-y_0,z-z_0] &= 0 \\ a(x-x_0)+b(y-y_0)+c(z-z_0) &= 0 \end{align*}\]

Nous sommes maintenant prêts à trouver l’équation du plan tangent à une surface. Pour simplifier la démonstration, nous allons modifier l’équation cartésienne d’un plan.

\[\begin{align*} a(x-x_0)+b(y-y_0)+c(z-z_0) &= 0 \\ c(z-z_0) &= -a(x-x_0)-b(y-y_0) \\ z-z_0 &= \frac{-a}{c}(x-x_0)+\frac{-b}{c}(y-y_0) \\ &= A(x-x_0)+B(y-y_0) \end{align*}\]

en posant \(A=-\frac{a}{c}\) et \(B=-\frac{b}{c}\).

Pour trouver les constantes \(A\) et \(B\), nous allons nous placer dans les plans \(y=y_0\) et \(x=x_0\). Tout d’abord, plaçons-nous dans le plan \(y=y_0\). Nous avons donc:

\[\begin{align*} z-z_0 &= A(x-x_0)+B(y_0-y_0) \\ z-z_0 &= A(x-x_0) \\ z &= Ax +(z_0-Ax_0) \end{align*}\]

L’équation précédente correspond à celle de la droite tangente à la courbe définie par \(z=f(x,y_0)\). La pente de cette droite correspond à la dérivée partielle de la fonction \(f\) par rapport à \(x\), évaluée en \((x_0,y_0)\), c’est-à-dire \(A=\left.\dfrac{\partial f}{\partial x}\right|_{(x_0,y_0)}\).

D’une manière similaire, nous montrons que \(B=\left.\dfrac{\partial f}{\partial y}\right|_{(x_0,y_0)}\).

L’équation du plan tangent est don donnée par:

\[ z = z_0 + \left.\dfrac{\partial f}{\partial x}\right|_{(x_0,y_0)}\cdot (x-x_0)+\left.\dfrac{\partial f}{\partial y}\right|_{(x_0,y_0)}\cdot (y-y_0) \]

Exemple 5.11 Trouvez l’équation du plan tangent à la surface \(f(x,y)=9-x^2-y^2\) au point \((1,1)\).

Exemple 5.12 Trouvez l’équation du plan tangent à la surface \(f(x,y)=\sin(xy)\) au point \(\left(\frac{\pi}{3},-1 \right)\).

Exemple 5.13 Trouvez le plan tangent horizontal à la surface \(f(x,y)=x^2-4xy-2y^2+12x-12y-1\)

Exemple 5.14 Trouvez l’équation du plan tangent à la surface \(f(x,y)=\dfrac{x-y}{x+y}\) au point \((1,1)\).

Remarque. Le plan tangent est l’analogue du polynôme de Taylor de degré 1 pour les fonctions de deux variables.