5.8 Le vecteur gradient

Nous allons maintenant définir une fonction vectorielle très utile, le vecteur gradient.

Définition 5.7 (Le vecteur gradient) Soit \(z=f(x,y)\) une fonction différentiable. Le gradient de \(f\), noté \(\nabla f\), est donné par: \[ \nabla f = \left[\dfrac{\partial f}{\partial x},\dfrac{\partial f}{\partial y}\right] \] Nous notons le gradient de \(f\) des façons suivantes: \(\nabla f\), \(\text{grad } f\) et \(\overrightarrow{\text{grad}} f\).

Le gradient d’une fonction est un vecteur.

Exemple 5.28 Trouvez le gradient de la fonction \(f(x,y)=x^2+3xy^5-4y^4\).

Exemple 5.29 Trouvez le gradient des fonctions suivantes:

1. \(f(x,y)=x^2-y^2\)
2. \(f(x,y)=\dfrac{x-y}{x+y}\)

Le vecteur gradient est très utile ccar celui-ci possède plusieurs caractéristiques intéressantes.

Théorème 5.5 Soit \(f(x,y)\) une fonction différentiable et \(\overrightarrow{u}\) un vecteur unitaire. Nous avons alors: \[ D_{\overrightarrow{u}} f = \nabla f \cdot \overrightarrow{u} \]

Preuve. Nous avons: \[\begin{align*} \nabla f \cdot \overrightarrow{u} &= \left[\dfrac{\partial f}{\partial x},\dfrac{\partial f}{\partial y}\right] \cdot [u_1,u_2] \\ &= \dfrac{\partial f}{\partial x}u_1 + \dfrac{\partial f}{\partial y}u_2 \\ &= D_{\overrightarrow{u}} f \end{align*}\] La dernière ligne est obtenue par le théorème 5.4.

Théorème 5.6 Le vecteur gradient d’une fonction \(f\) pointe dans la direction d’accroissement maximal de celle-ci. De plus, le taux de variation dans cette direction est donné par la norme du gradient.

Preuve. Soit un vecteur unitaire \(\overrightarrow{u}\). La dérivée directionnelle de \(f\) dans la direction de \(\overrightarrow{u}\) est donnée par \(D_{\overrightarrow{u}} f = \nabla f \cdot \overrightarrow{u}\). Nous voulons trouvez \(\overrightarrow{u}\) tel que cette dérivée est maximale. Nous savons que: \[\begin{align*} \nabla f \cdot \overrightarrow{u} &= ||\nabla f || \cdot ||\overrightarrow{u} || \cos(\theta) \\ &= ||\nabla f || \cos(\theta) \quad \text{car $\overrightarrow{u}$ est unitaire} \end{align*}\] où \(\theta\) est l’angle entre \(\nabla f\) et \(\overrightarrow{u}\). Le membre de droite est maximal si \(\cos(\theta)=1\), c’est-à-dire lorsque \(\theta=0\). D’où la direction maximale est celle donnée par le vecteur gradient.

De plus, dans cette direction, la dérivée directionnelle est \(D_{\overrightarrow{u}} f=||\nabla f ||\).

Exemple 5.30 Soit la fonction \(f(x,y)=xe^{-x^2-y^2}\). Déterminez la direction dans laquelle se trouve l’accroissement maximal au point \((1,1)\) et le taux de variation maximal.

Exemple 5.31 Soit la fonction \(f(x,y)=(x+y^2)e^{-x}\). Déterminez la direction dans laquelle se trouve l’accroissement maximal au point \((1,1)\) et le taux de variation maximal.

La dernière propriété que nous verrons concernant le vecteur gradient met en relation celui-ci avec les courbes de niveau d’une fonction.

Théorème 5.7 Le vecteur gradient d’une fonction est perpendiculaire aux courbes de niveaux de cette fonction.

Preuve. Soit un point \((x_0,y_0)\) du domaine de la fonction \(f\). Soit \(\overrightarrow{u}\) un vecteur unitaire pointant dans la direction de la courbe de niveau passant par le point \((x_0,y_0)\). La figure 5.3 représente cette situation.

À ce moment, nous avons \(D_{\overrightarrow{u}} f(x_0,y_0)=0\), car la fonction ne varie pas le long d’une courbe de niveau. Nous pouvons également écrire \(D_{\overrightarrow{u}} f(x_0,y_0)=0=||\nabla f(x_0,y_0)||\cos(\theta)\), où \(\theta\) est l’angle entre le vecteur gradient et \(\overrightarrow{u}\). Puisque \(||\nabla f(x_0,y_0)||\) n’est pas obligatoirement nul, nous avons que: \[ \cos(\theta) = 0 \Longrightarrow \theta=\dfrac{\pi}{2} \] Ainsi, le gradient est perpendiculaire aux courbes de niveaux.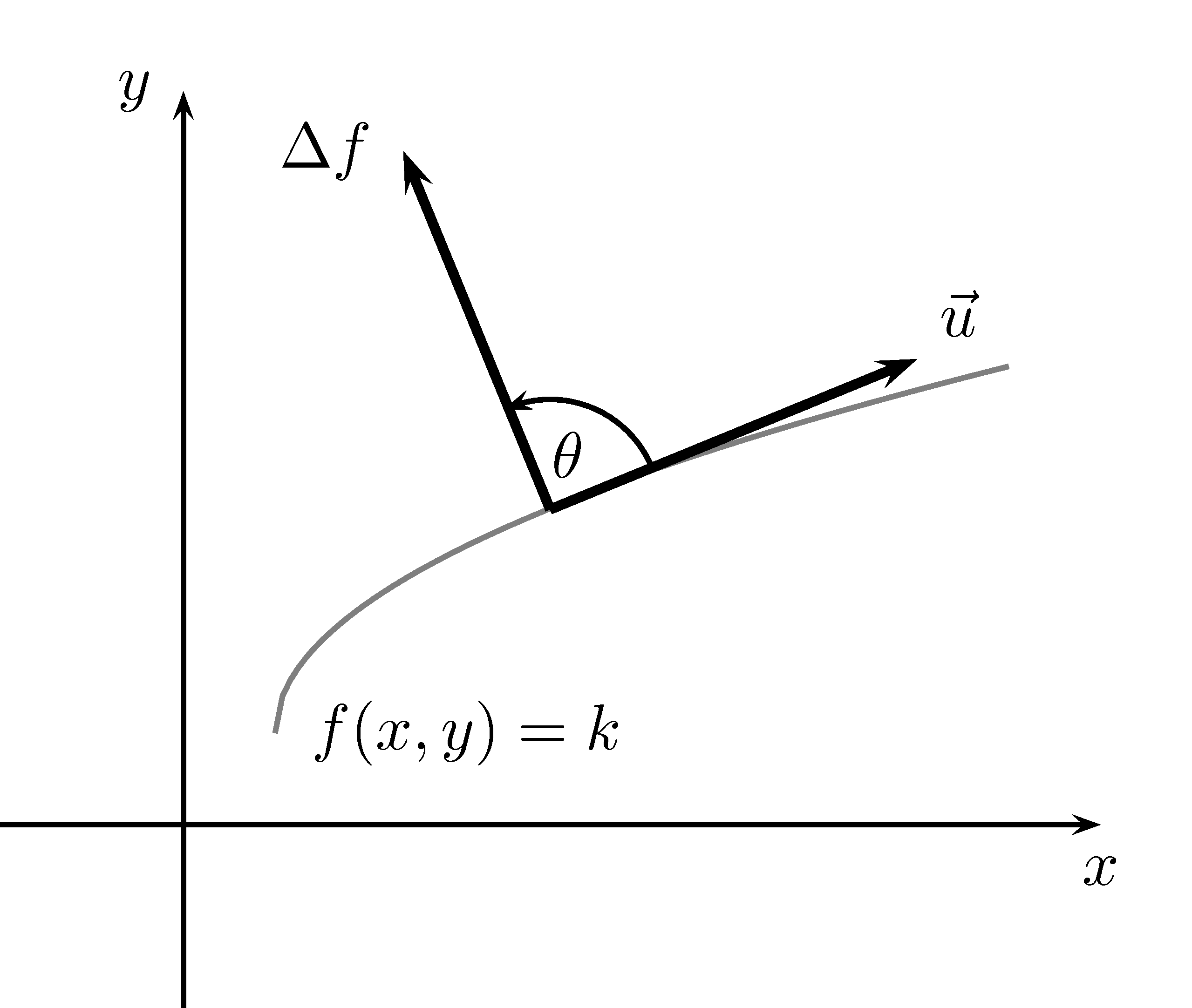

Figure 5.3: Représentation d’une courbe de niveau et du gradient.

5.8.1 Le gradient des fonctions de plus de deux variables

Les notions de dérivée directionnelle et de gradient se généralisent pour les fonctions de plus de deux variables. Ainsi, si \(z=f(x_1,x_2,\ldots, x_n)\), nous avons que:

\[ \nabla f = \left[\dfrac{\partial f}{\partial x_1},\dfrac{\partial f}{\partial x_2},\ldots,\dfrac{\partial f}{\partial x_n}\right] \]

Cette généralisation nous permet de simplifier la résolution de certains problèmes.

Exemple 5.32 Trouvez l’équation du plan tangent à la surface définie par \(xyz=1\) en \(x=1\) et \(y=1\).

Exemple 5.33 Trouvez l’équation du plan tangent à la surface définie par \(x^2+y-z^3=1\) en \(x=1\) et \(y=1\).