4.3 Graphique
Lorsque nous avons une fonction \(y=f(x)\), son graphe correspond à une courbe dans le plan cartésien, c’est-à-dire dans \(\mathbb{R}^2\). Pour parvenir à dessiner cette courbe, on fait correspondre une valeur de \(y\) pour chaque valeur de \(x\).
Lorsque nous somme en présence d’une fonction de deux variables \(z=f(x,y)\), le graphique de cette fonction est une surface dans l’espace de trois dimensions, \(\mathbb{R}^3\).
Par contre, lorsque notre fonction possède plus de deux variables, il devient difficile, voire impossible de la représenter graphiquement. Il faudrait utiliser des espaces de plus de trois dimensions.
La figure 4.2 montre de quelle façon nous pouvons représenter le point (a,b,f(a,b)) dans l’espace à trois dimensions.
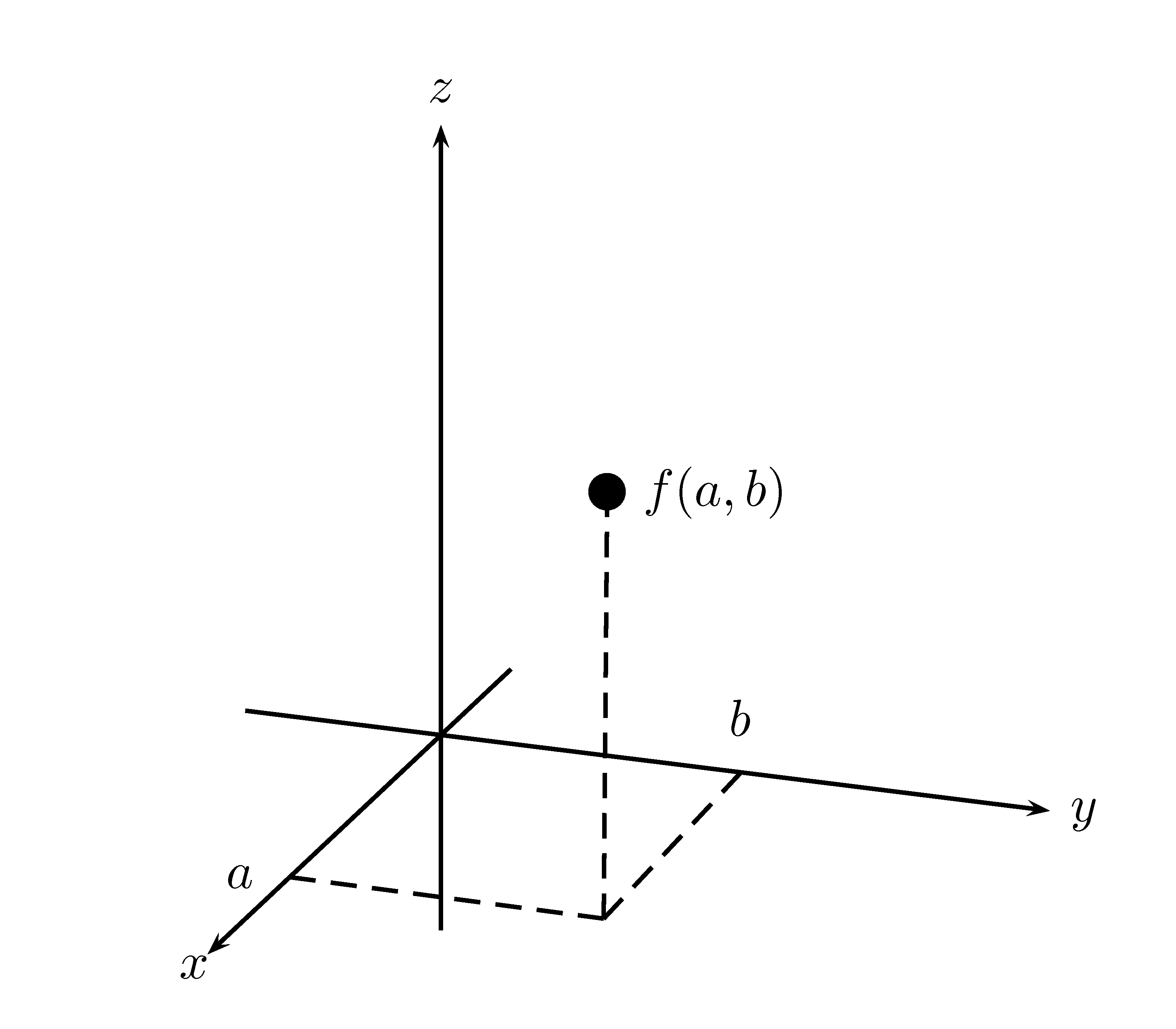
Figure 4.2: Représentation en trois dimensions d’un point.
Nous allons maintenant présenter plusieurs fonctions accompagnées de leur graphique.
Les figures suivantes représentent des fonctions usuelles que nous rencontrerons régulièrement dans le cours.
Figure 4.3: Plan: \(z=1-x-y\)
Figure 4.4: Paraboloïde: \(z=x^2+y^2\)
Figure 4.5: Hyperboloïde : \(z=(x^2-y^2)/2\)
Figure 4.6: Cône : \(z=\sqrt{x^2+y^2}\)
Figure 4.7: Sphère: \(x^2+y^2+z^2=R^2\)
Figure 4.8: Ellipse: \(\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}+\dfrac{z^2}{c^2}=1\)
Figure 4.9: Hyperboloïde à une nappe: \(\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}-\dfrac{z^2}{c^2}=1\)
Figure 4.10: Hyperboloïde à deux nappes: \(-\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}+\dfrac{z^2}{c^2}=1\)
Figure 4.11: Tore: \((x^2+y^2+z^2+a^2-r^2)^2=4 a^2(x^2+y^2)\)