7.3 Les intégrales doubles en coordonnéees polaires

Dans certains cas, il est difficile de calculer certaines intégrales en coordonnées cartésiennes et ce, pour différentes raisons. Parfois le domaine d’intégration est difficile à écrire en coordonnées cartésiennes. Par exemple, si le domaine d’intégration est celui présenté à la figure 7.6, il serait alors plus simple d’utiliser les coordonnées polaires.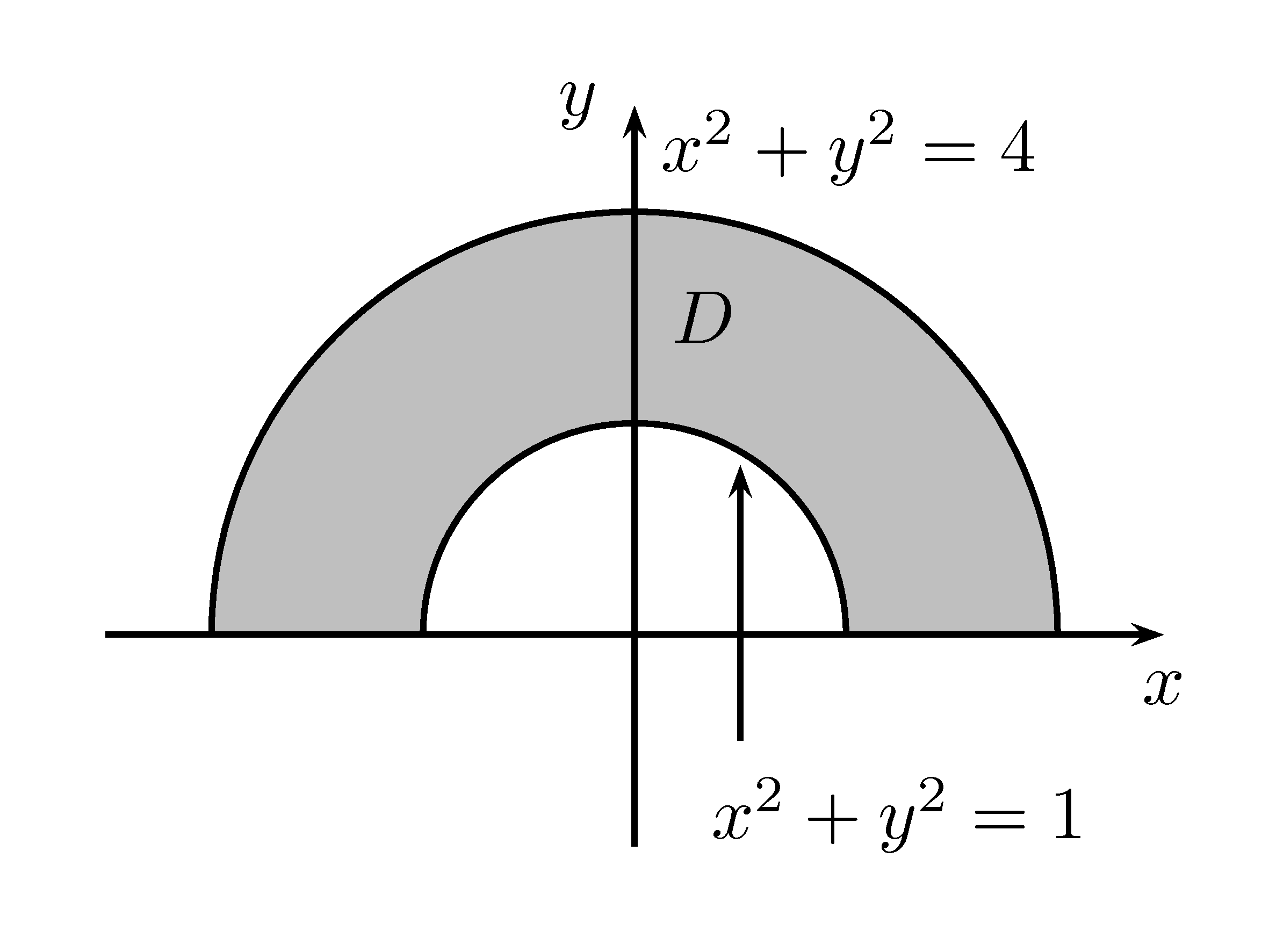

Figure 7.6: Une région sur laquelle nous voulons intégrer qui se prête particulièrement bien aux coordonnées polaires.

Voyons comment nous pouvons effectuer le changement de coordonnées. Supposons tout d’abord que le domaine est un rectangle polaire, c’est-à-dire que: \[D=\{(r,\theta)|a\leq r\leq b,\alpha \leq \theta\leq \beta\}\] Divisons maintenant ce rectangle polaire en petits rectangles polaires. Posons \[\begin{align*} R_{i,j}&=\{(r,\theta)|r_{i-1}\leq r\leq r_{i},\theta_{j-1} \leq \theta\leq \theta_j \},\\ \Delta \theta_j&=\theta_j-\theta_{j-1},\\ \Delta r_i&=r_i-r_{i-1}. \end{align*}\] La figure 7.7 représente un rectangle polaire ainsi qu’une partition possible de ce rectangle.

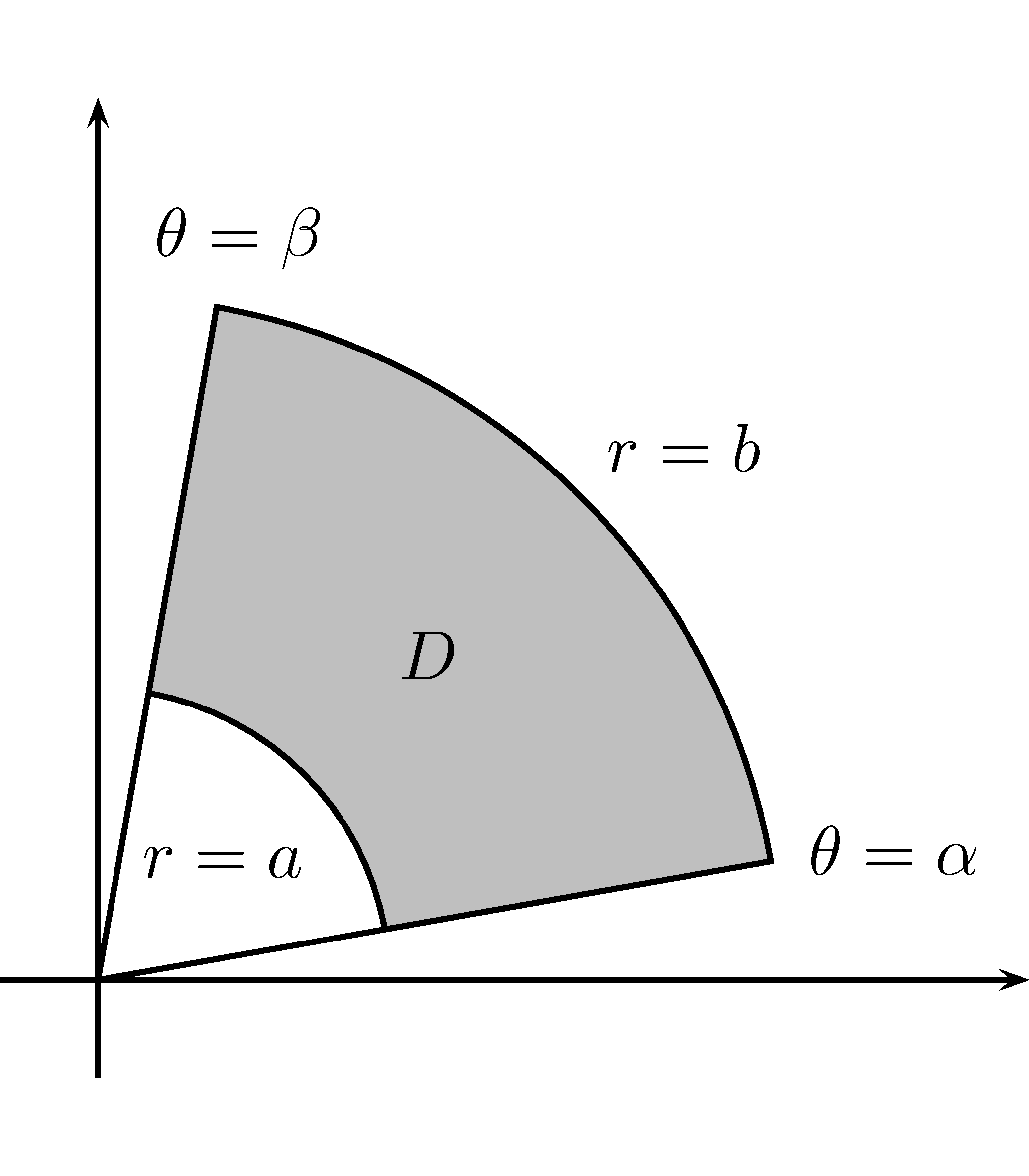
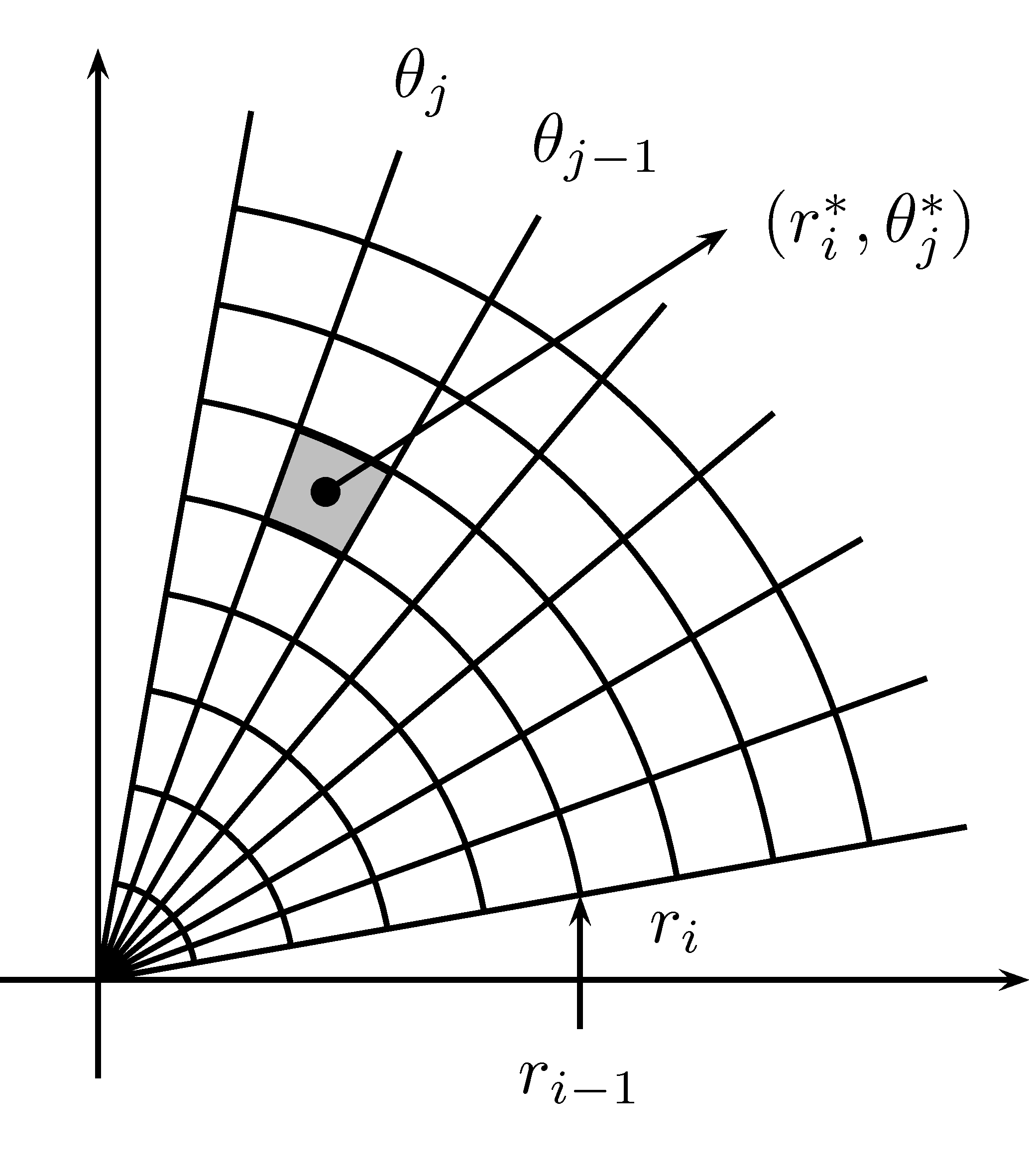
Figure 7.7: Un rectangle polaire et une partition du rectangle polaire.

Le volume délimité par le rectangle polaire \(R_{ij}\) et la fonction \(f(x,y)\) est donné par: \[\begin{align*} V_{ij}&\approx f(x_i^*,y_j^*)\Delta A_{i,j}\\ &\approx f(r_i^*\cos \theta_j^*,r_i^*\sin \theta_j^*)\Delta A_{i,j} \end{align*}\] où \((r_i^*,\theta_j^*)\) est le point au centre de \(R_{i,j}\). Il ne reste plus qu’à déterminer \(\Delta A_{i,j}\) qui correspond à l’aire de \(R_{i,j}\). Nous savons que l’aire d’une section de disque de rayon \(R\) est donnée par: \[\begin{align*} A=\dfrac{1}{2}R^2\varphi \end{align*}\] où \(\varphi\) est l’angle au centre. Ainsi, nous pouvons trouver \(\Delta A_{i,j}\) en effectuant la différence de l’aire deux sections. D’où: \[\begin{align*} \Delta A_{i,j}= \frac{1}{2}r_i^2\Delta \theta_j-\frac{1}{2}r_{i-1}^2\Delta \theta_j. \end{align*}\] Nous allons manipuler l’expression précédente pour la simplifier. \[\begin{align*} \Delta A_{i,j}&= \frac{1}{2}r_i^2\Delta \theta_j-\frac{1}{2}r_{i-1}^2\Delta \theta_j\\ &= \frac{1}{2}\left(r_i^2- r_{i-1}^2 \right)\theta_j\\ &= \underbrace{\frac{1}{2}(r_i+r_{i-1})}_{=r_i^*}\underbrace{(r_i-r_{i-1})}_{=\Delta r_i} \Delta \theta_j \\ &=r_i^*\Delta r_i\Delta \theta_j. \end{align*}\] Ainsi, \[\begin{align*} V_{i,j}\approx f(r_i^*\cos \theta_j^*,r_i^*\sin \theta_j^*)r_i^*\Delta r_i\Delta \theta_j \end{align*}\] Posons \(g(r,\theta)=rf(r\cos\theta, r\sin\theta)\). Maintenant, trouvons une expression pour l’intégrale double. \[\begin{align*} \iint\limits_Df(x,y)dA&:=\lim_{m,n\to\infty }\sum_{i=1}^n\sum_{j=1}^mf(r_i^*\cos \theta_j^*,r_i^*\sin \theta_j^*)\Delta A_{i,j}\\ &=\lim_{m,n\to\infty }\sum_{i=1}^n\sum_{j=1}^mg(r_i^*,\theta_j^*)\Delta r_i\Delta \theta_j\\ &=\int_{\alpha }^{\beta }\int_{a }^{b }g(r,\theta)drd\theta\\ &=\int_{\alpha }^{\beta }\int_{a }^{b }f(r\cos\theta,r\sin\theta)rdrd\theta \end{align*}\]

Remarque. Il est important de voir que \(dxdy=rdrd\theta\). Ainsi, nous devons multiplier la fonction par \(r\) lorsque nous passons en coordonnées polaires.

Exemple 7.16 Trouvez \(\iint\limits_D (x^2+y^2)dA\) sur le disque de rayon 1 centré à l’origine.

Exemple 7.17 Trouvez \(\iint\limits_D \frac{1}{e^{x^2+y^2}}dA\) sur le quart de disque de rayon 3 centré à l’origine.

Nous avons montré le changement en coordonnées polaires lorsque le domaine est un rectangle polaire. Cependant, tout comme pour les coordonnées cartésiennes, il est possible de fixer une variable et de faire varier l’autre, ce qui entraîne que les bornes peuvent dépendre d’une variable. La figure 7.8 présente les deux possibilités, que la variable \(r\) dépende de \(\theta\) ou que la variable \(\theta\) dépende de \(r\).

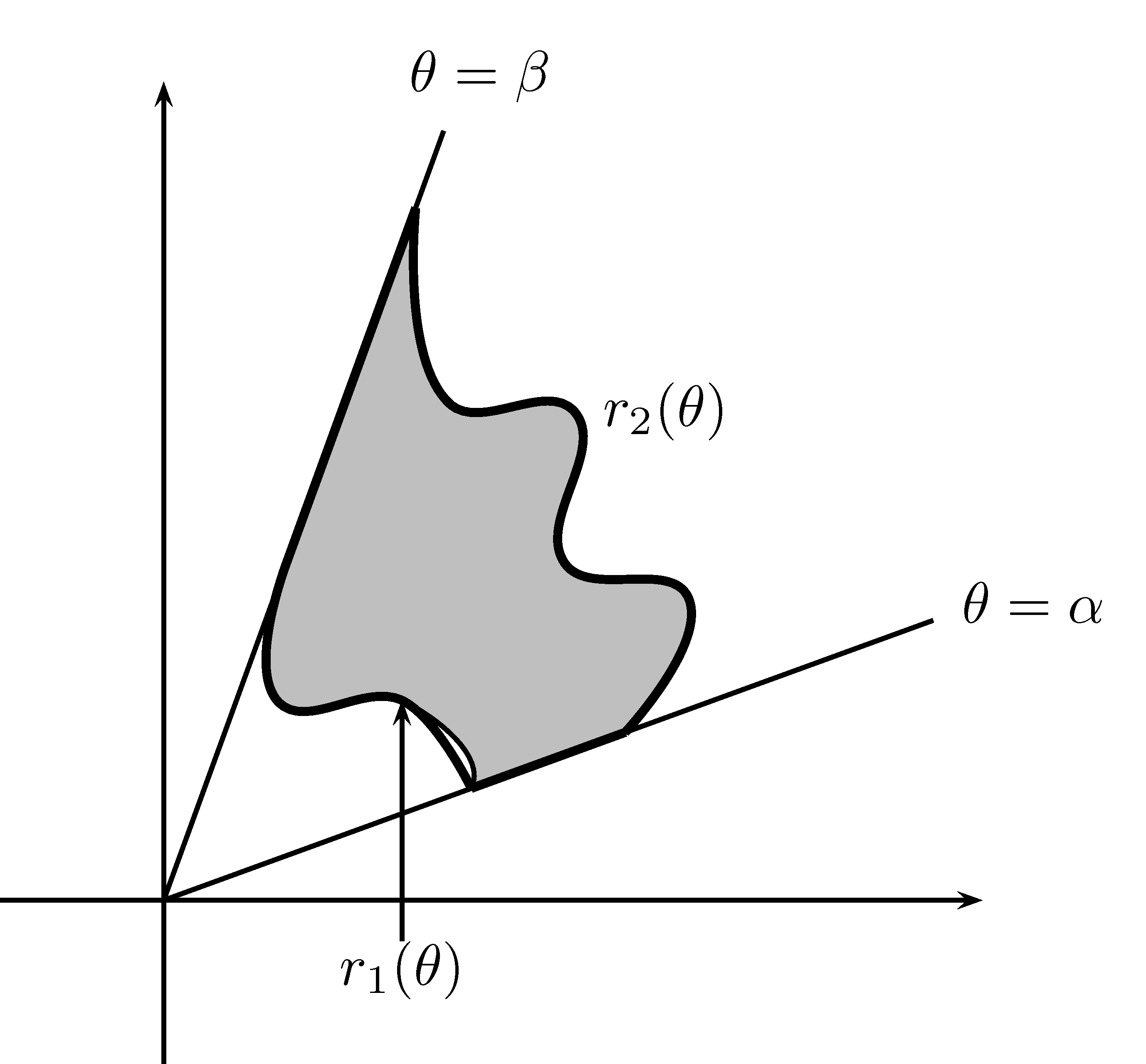
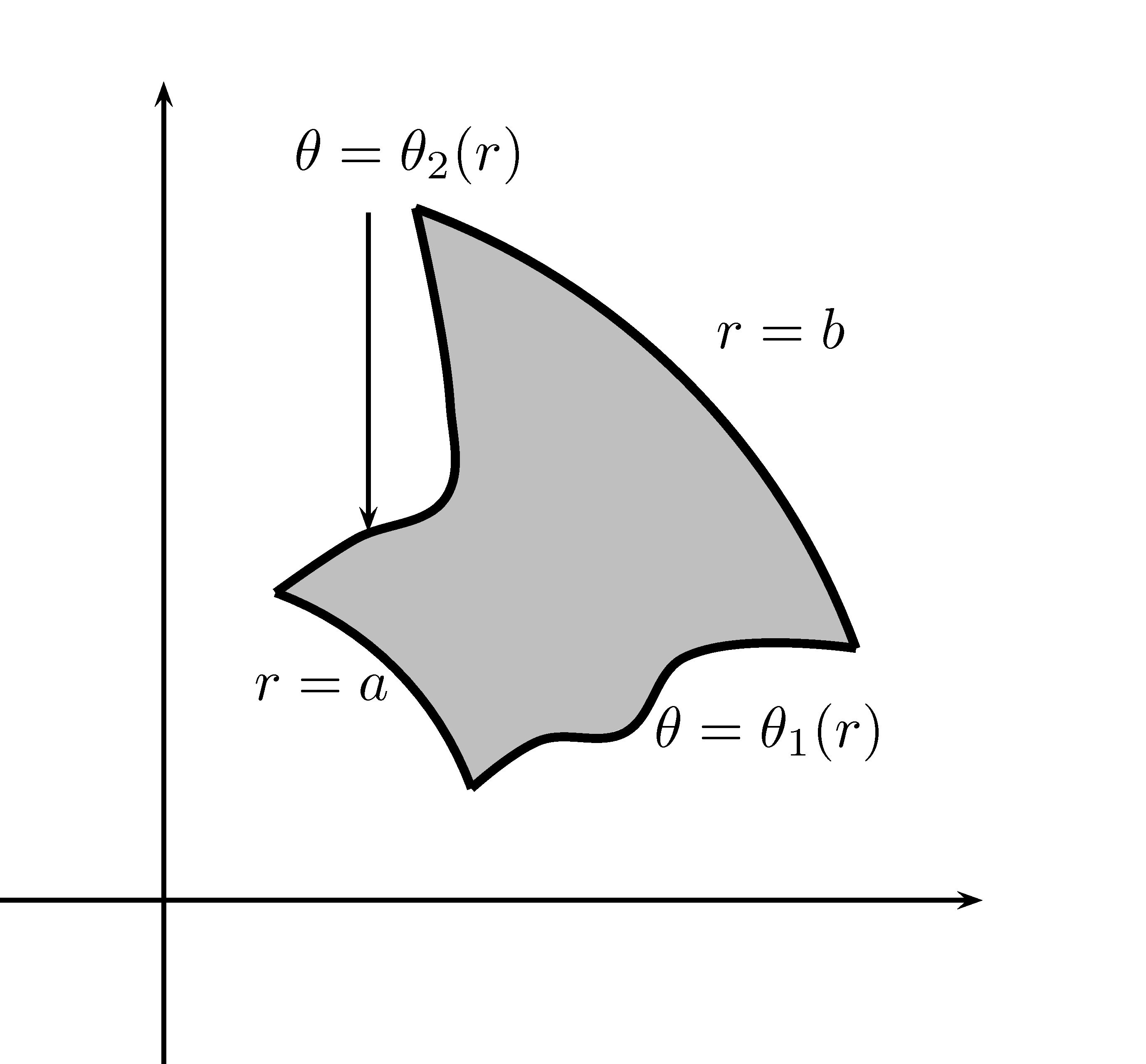
Figure 7.8: La variable \(r\) peut dépendre de \(\theta\) et vice-versa.

Dans le cas de la figure 7.8 de gauche, l’intégrale devient: \[\begin{align*} \iint\limits_D f(x,y)dA=\int_{\alpha }^{\beta}\int_{r_1(\theta)}^{r_2(\theta)}f(r\cos\theta,r\sin\theta)rdrd\theta \end{align*}\] Dans le cas de la figure 7.8 de droite, l’intégrale devient: \[\begin{align*} \iint\limits_Df(x,y)dA=\int_{a}^{b}\int_{\theta_1(r)}^{\theta_2(r)}f(r\cos\theta,r\sin\theta)rd\theta dr \end{align*}\]

Remarque. Nous allons nous intéresser à un cas particulier. Soit \(f(x,y)=1\), alors l’inttégrale double calcule maintenant la surface du domaine d’intégration. Si nous nous plaçons dans le premier cas où la variable \(r\) dépend de \(\theta\), c’est-à-dire \(r_1(\theta)=0\) et \(r_2(\theta)=r(\theta)\) pour \(\alpha \leq \theta \leq \beta\), nous obtenons: \[\begin{align*} \text{Aire}(D)&=\int_{\alpha }^{\beta }\int_0^{r(\theta)}rdrd\theta\\ &=\int_{\alpha }^{\beta }\left.\dfrac{r^2}{2}\right|_0^{r(\theta)}d\theta\\ &=\int_{\alpha }^{\beta }\dfrac{r^2(\theta)}{2}\theta \end{align*}\] L’équation précédente correspond au résultat obtenu au chapitre 3 pour le calcul de l’aire d’une région polaire.

Exemple 7.18 Trouvez \(\int_0^1 \int_y^{\sqrt{2-y^2}} (x^2+y^2) dx dy\).

Exemple 7.19 Trouvez \(\iint\limits_D \frac{1}{\sqrt{x^2+y^2}}dA\) sur la région bornée par \(y=\sqrt{3}x\), \(x=3\) et \(y=0\).

Exemple 7.20 Déterminez l’aire de la région située entre \(r=3+2\sin(\theta)\) et \(r=2\).