8.3 Intégrales triples en coordonnées cylindriques

Nous allons débuter en introduisant les coordonnées cylindriques.

Définition 8.1 (Coordonnées cylindriques) Soit un point \((x,y,z)\in\mathbb{R}^3\) en coordonnées cartésiennes. Nous pouvons représenter ce point en coordonnées cylindriques en effectuant les transformations suivantes: \[\begin{align*} x &= r\cos(\theta) \\ y &= r\sin(\theta) \\ z &= z \end{align*}\] avec les conditions suivantes: \[\begin{align*} 0 \leq r \leq \infty \\ 0 \leq \theta \leq 2\pi \\ -\infty \leq z \leq \infty \end{align*}\]

La figure 8.1 représente un point en coordonnées cylindriques.

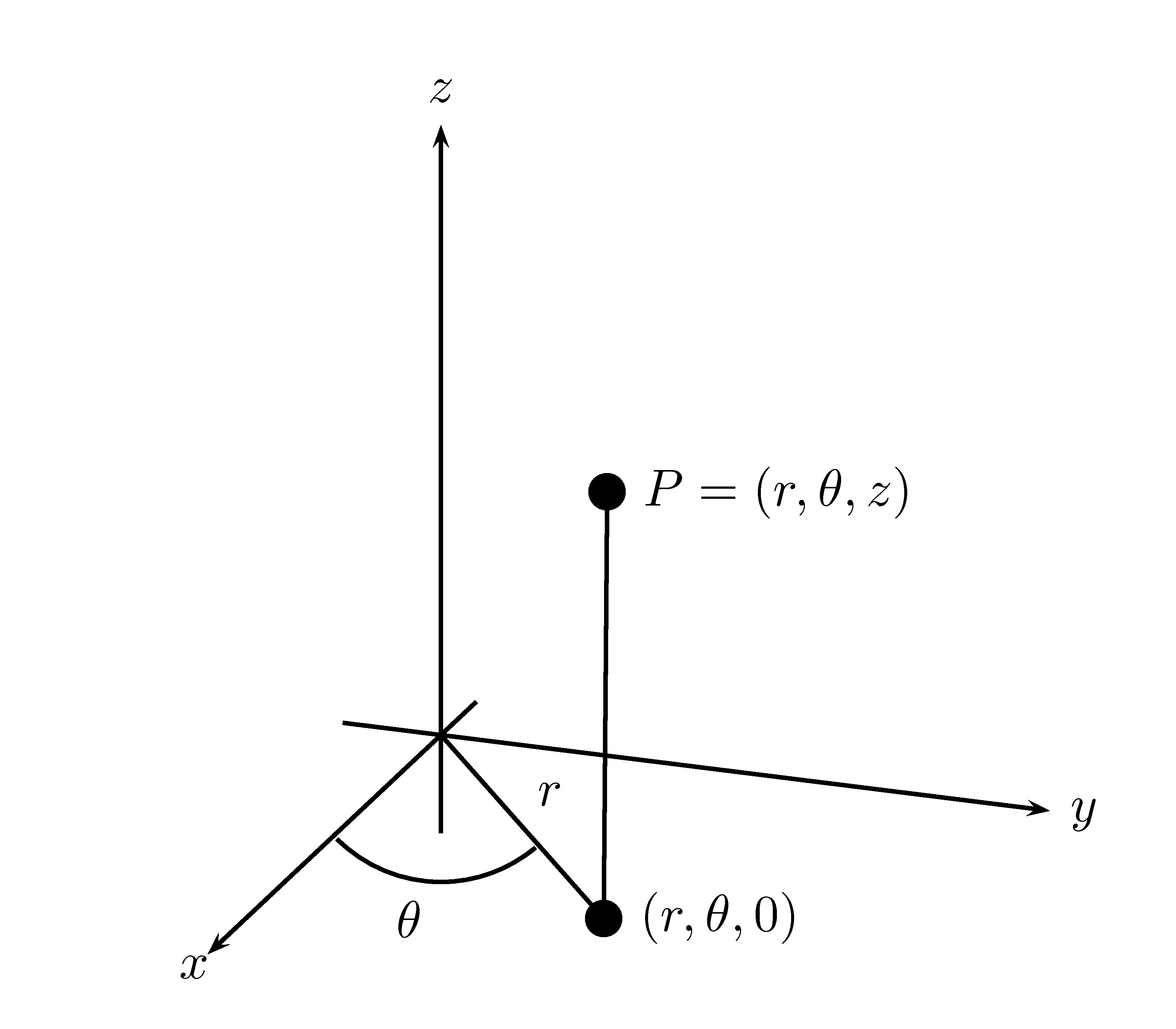
Figure 8.1: Un point \(P\) représenté en coordonnées cylindriques.

Remarque. Les coordonnées cylindriques sont en fait des coordonnées polaires pour les variables \(x\) et \(y\) et nous conservons \(z\) en coordonnées cartésiennes. Nous pouvons remarquer que \(x^2+y^2=r^2\).

De façon analogue à la démonstration faite à la section 7.3 pour les coordonnées polaires, nous pouvons montrer que \[\iiint\limits_V f(x,y,z)dV=\iiint\limits_V f(r\cos(\theta),r\sin(\theta) ,z) r drd\theta dz\]

Exemple 8.7 Calculez le volume d’un morceau fromage coupé dans un cylindre de 4 cm de hauteur, de 6 cm de rayon et d’angle \(\frac{\pi}{4}\).

Exemple 8.8 Calculez le volume entre les paraboloïdes \(z=4-x^2-y^2\) et \(z=x^2+y^2\).

Exemple 8.9 Trouvez le volume du solide délimité par l’intérieur de la sphère \(x^2+y^2+z^2=6\) et au-dessus du paraboloïde \(z=x^2+y^2\).

Exemple 8.10 Trouvez le volume de la demi-sphère de rayon \(a\) se situant à l’extérieur du cylindre \(r=\frac{a}{2}\).

Exemple 8.11 Trouvez le volume du cône tronqué \(z=9-\sqrt{x^2+y^2}\) avec \(0\leq z \leq 4\).