6.4 La droite de régression
Supposons que nous ayons amassé \(n\) couples de données \((x_i,y_i)\) pour \(i\in \{1,2,\ldots, n\}\). Nous voulons déterminer l’équation de laa droite qui minimise la somme des carrés des distances verticales entre les points et cette droite. En d’autre mots, nous voulons trouver l’équation de la droite la plus proche du nuage de points. Cette situation est représentée à la figure 6.3.
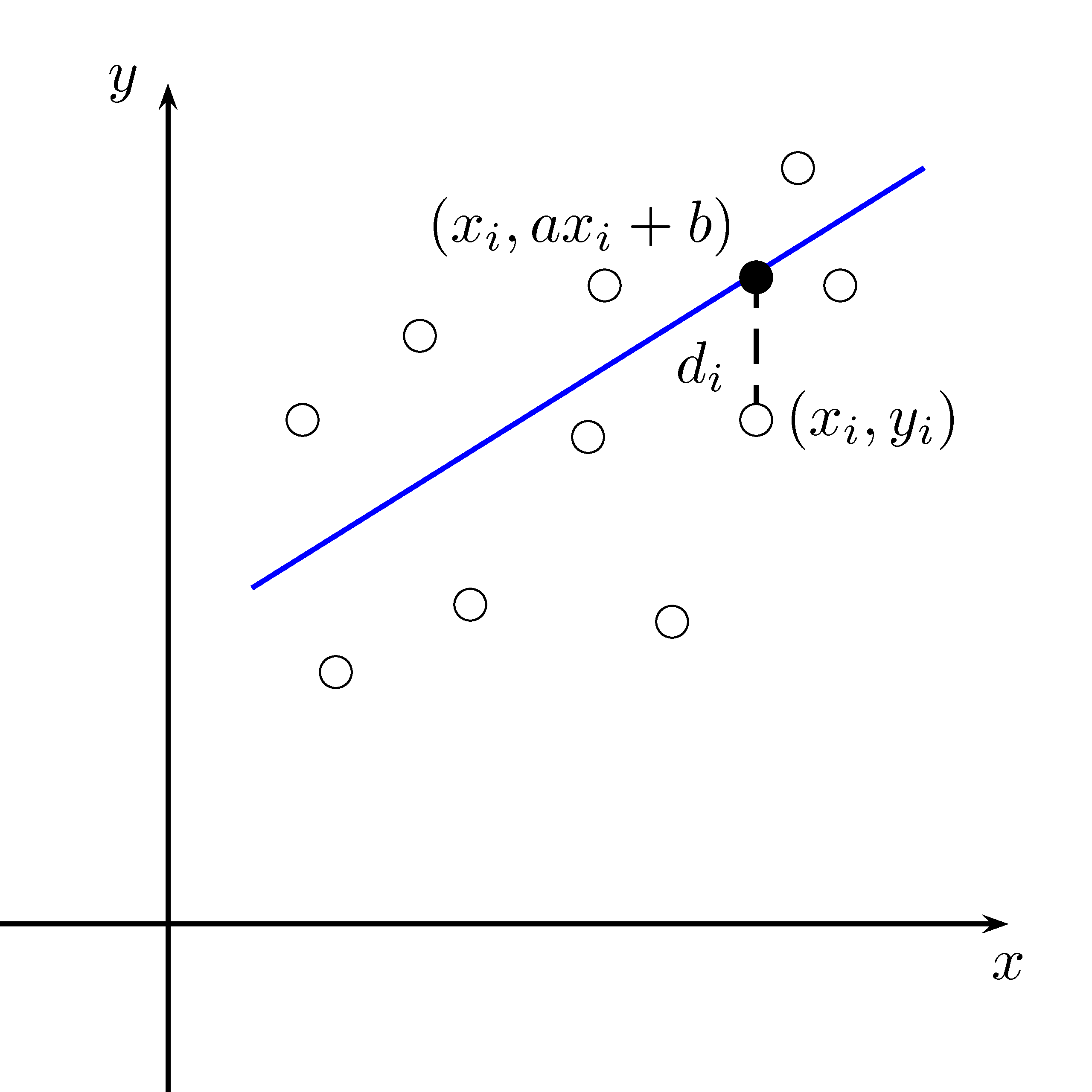
Figure 6.3: Nuage de points et droite de régression
Nous allons supposer que l’équation est de la forme \(y=ax+b\) avec \(a\) et \(b\) que nous devons déterminer en minimisant la somme des carrés des distances verticales. Nous savons:
\[ d_i^2 = (y-y_i)^2 = (ax_i+b-y_i)^2 \]
Nous voulons minimiser la somme de toutes ces distances, c’est-à-dire:
\[\begin{equation} \begin{split} f(a,b) &= \sum_{i=1}^n d_i^2 \notag \\ &= \sum_{i=1}^n (ax_i+b-y_i)^2 \end{split} \tag{6.2} \end{equation}\]Nous désirons trouver \(a\) et \(b\) tels qu’ils minimisent la fonction \(f(a,b)\). Nous désirons en fait trouver les points critiques de \(f\):
\[\begin{align} \dfrac{\partial f}{\partial a} &= \sum_{i=1}^n 2x_i(ax_i+b-y_i) = 0 \tag{6.3}\\ \dfrac{\partial f}{\partial b} &= \sum_{i=1}^n 2(ax_i+b-y_i) = 0 \tag{6.4} \end{align}\]En utilisant l’équation (6.4), nous obtenons:
\[\begin{align} \sum_{i=1}^n 2(ax_i+b-y_i) &= 0 \notag\\ \sum_{i=1}^n 2ax_i + \sum_{i=1}^n 2b - \sum_{i=1}^n 2y_i &= 0 \notag\\ b \sum_{i=1}^n 1 &= \sum_{i=1}^n y_i - a \sum_{i=1}^n x_i \notag\\ bn &= \sum_{i=1}^n y_i - a \sum_{i=1}^n x_i \notag\\ b &= \dfrac{\sum\limits_{i=1}^n y_i - a \sum\limits_{i=1}^n x_i}{n} \tag{6.5} \end{align}\]Nous devons maintenant remplacer l’équation (6.5) dans l’équation (6.3).
\[\begin{align*} \sum_{i=1}^n 2x_i(ax_i+b-y_i) &= 0 \\ a\sum_{i=1}^n x_i^2 + b \sum_{i=1}^n x_i - \sum_{i=1}^n x_iy_i &= 0 \\ a\sum_{i=1}^n x_i^2 + \left(\dfrac{\sum\limits_{i=1}^n y_i - a \sum\limits_{i=1}^n x_i}{n}\right) \sum_{i=1}^n x_i - \sum_{i=1}^n x_iy_i &= 0 \\ an\sum_{i=1}^n x_i^2+\left(\sum_{i=1}^n x_i\right)\left(\sum_{i=1}^n y_i\right)-a\left(\sum_{i=1}^n x_i\right)^2- \sum_{i=1}^n x_iy_i &= 0 \\ a\left(n\sum_{i=1}^n x_i^2-\left(\sum_{i=1}^n x_i\right)^2\right) &= \sum_{i=1}^n x_iy_i-\left(\sum_{i=1}^n x_i\right)\left(\sum_{i=1}^n y_i\right) \\ a &= \dfrac{\sum\limits_{i=1}^n x_iy_i-\left(\sum\limits_{i=1}^n x_i\right)\left(\sum\limits_{i=1}^n y_i\right)}{n\sum\limits_{i=1}^n x_i^2-\left(\sum\limits_{i=1}^n x_i\right)^2} \end{align*}\]En résumé, nous avons:
\[\begin{align*} a &= \dfrac{\sum\limits_{i=1}^n x_iy_i-\left(\sum\limits_{i=1}^n x_i\right)\left(\sum\limits_{i=1}^n y_i\right)}{n\sum\limits_{i=1}^n x_i^2-\left(\sum\limits_{i=1}^n x_i\right)^2} \\ b &= \dfrac{\sum\limits_{i=1}^n y_i - a \sum\limits_{i=1}^n x_i}{n} \end{align*}\]En utilisant le théorème 6.2, nous pourrions démontrer que ces valeurs de \(a\) et \(b\) minimisent la fonction \(f\).
| x | y |
|---|---|
| 10 | 8.04 |
| 8 | 6.95 |
| 13 | 7.58 |
| 9 | 8.81 |
| 11 | 8.33 |
| 14 | 9.96 |
| 6 | 7.24 |
| 4 | 4.26 |
| 12 | 10.84 |
| 7 | 4.82 |
| 5 | 5.68 |
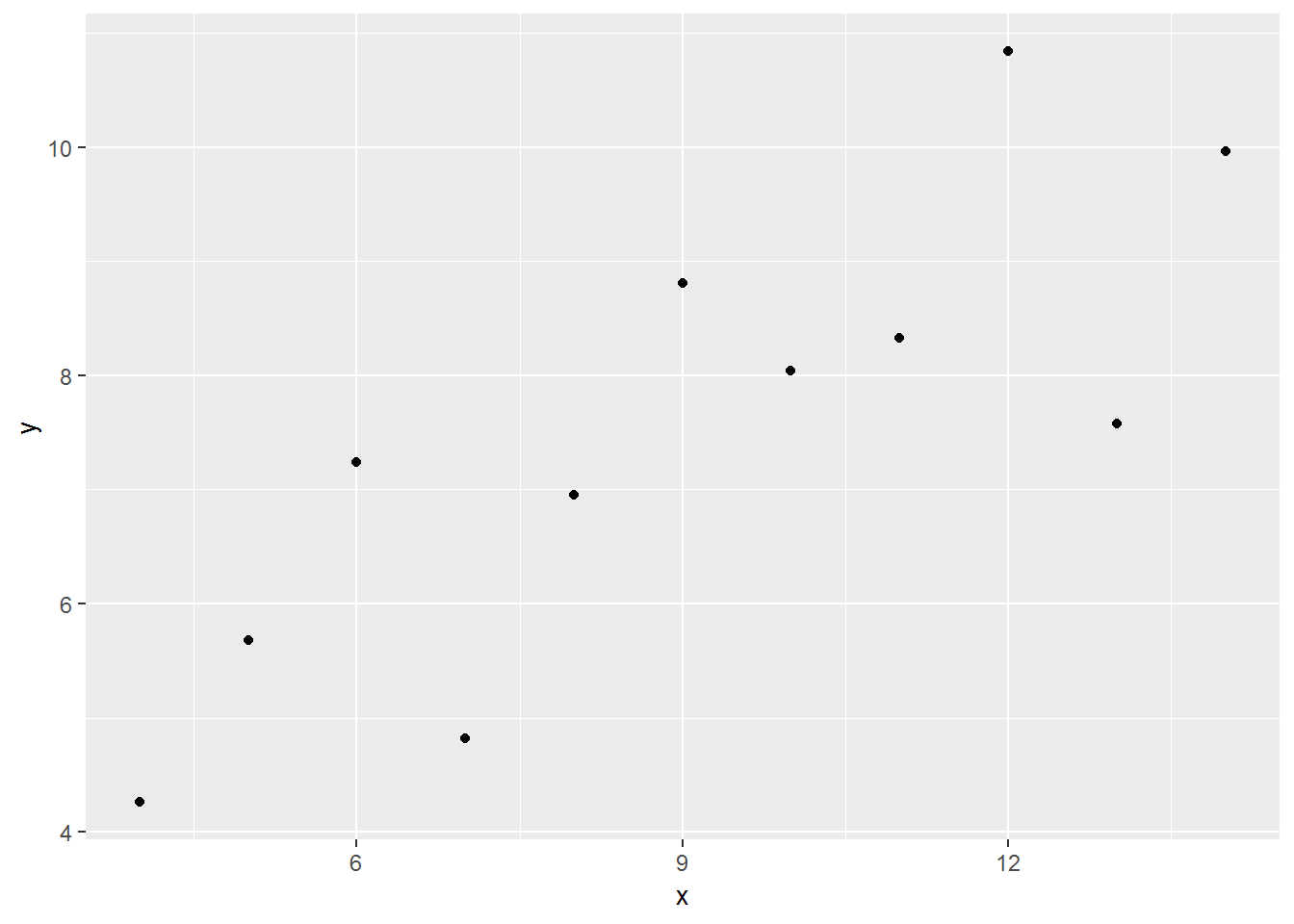
Figure 6.4: Le nuage de points.
6.4.1 Le quartet d’Anscombe
Le quartet d’Anscombe est constitué de quatre ensembles de données qui ont les mêmes propriétés statistiques simples mais qui sont en réalité très différents, ce qui se voit facilement lorsqu’on les représente sous forme de graphiques. Ils ont été construits en 1973 par le statisticien Francis Anscombe dans le but de démontrer l’importance de tracer des graphiques avant d’analyser des données, car cela permet notamment d’estimer l’incidence des données aberrantes sur les différentes indices statistiques que l’on pourrait calculer.
Dans la table 6.1, les observations \(x_i\) sont reliées aux observations \(y_i\).
| x1 | x2 | x3 | x4 | y1 | y2 | y3 | y4 |
|---|---|---|---|---|---|---|---|
| 10 | 10 | 10 | 8 | 8.04 | 9.14 | 7.46 | 6.58 |
| 8 | 8 | 8 | 8 | 6.95 | 8.14 | 6.77 | 5.76 |
| 13 | 13 | 13 | 8 | 7.58 | 8.74 | 12.74 | 7.71 |
| 9 | 9 | 9 | 8 | 8.81 | 8.77 | 7.11 | 8.84 |
| 11 | 11 | 11 | 8 | 8.33 | 9.26 | 7.81 | 8.47 |
| 14 | 14 | 14 | 8 | 9.96 | 8.10 | 8.84 | 7.04 |
| 6 | 6 | 6 | 8 | 7.24 | 6.13 | 6.08 | 5.25 |
| 4 | 4 | 4 | 19 | 4.26 | 3.10 | 5.39 | 12.50 |
| 12 | 12 | 12 | 8 | 10.84 | 9.13 | 8.15 | 5.56 |
| 7 | 7 | 7 | 8 | 4.82 | 7.26 | 6.42 | 7.91 |
| 5 | 5 | 5 | 8 | 5.68 | 4.74 | 5.73 | 6.89 |
Avant d’afficher les ensembles de données, nous allons calculer quelques mesures sur chacun de ces ensembles, à savoir, la moyenne des \(x\), la moyenne des \(y\), la variance des \(x\), la variance des \(y\) et le coefficient de corrélation.
| ensemble | moyenne des \(x\) | variance des \(x\) | moyenne des \(y\) | variance des \(y\) | coeff. de corrélation |
|---|---|---|---|---|---|
| I | 9 | 11 | 7.500909 | 4.127269 | 0.8164205 |
| II | 9 | 11 | 7.500909 | 4.127629 | 0.8162365 |
| III | 9 | 11 | 7.500000 | 4.122620 | 0.8162867 |
| IV | 9 | 11 | 7.500909 | 4.123249 | 0.8165214 |
Comme nous pouvons le remarquer, les quatre ensembles de données possèdent les mêmes mesures. Par contre, lorsque nous affichons ensuite les quatre ensembles de données, nous remarquons que ces ensembles sont très différents.
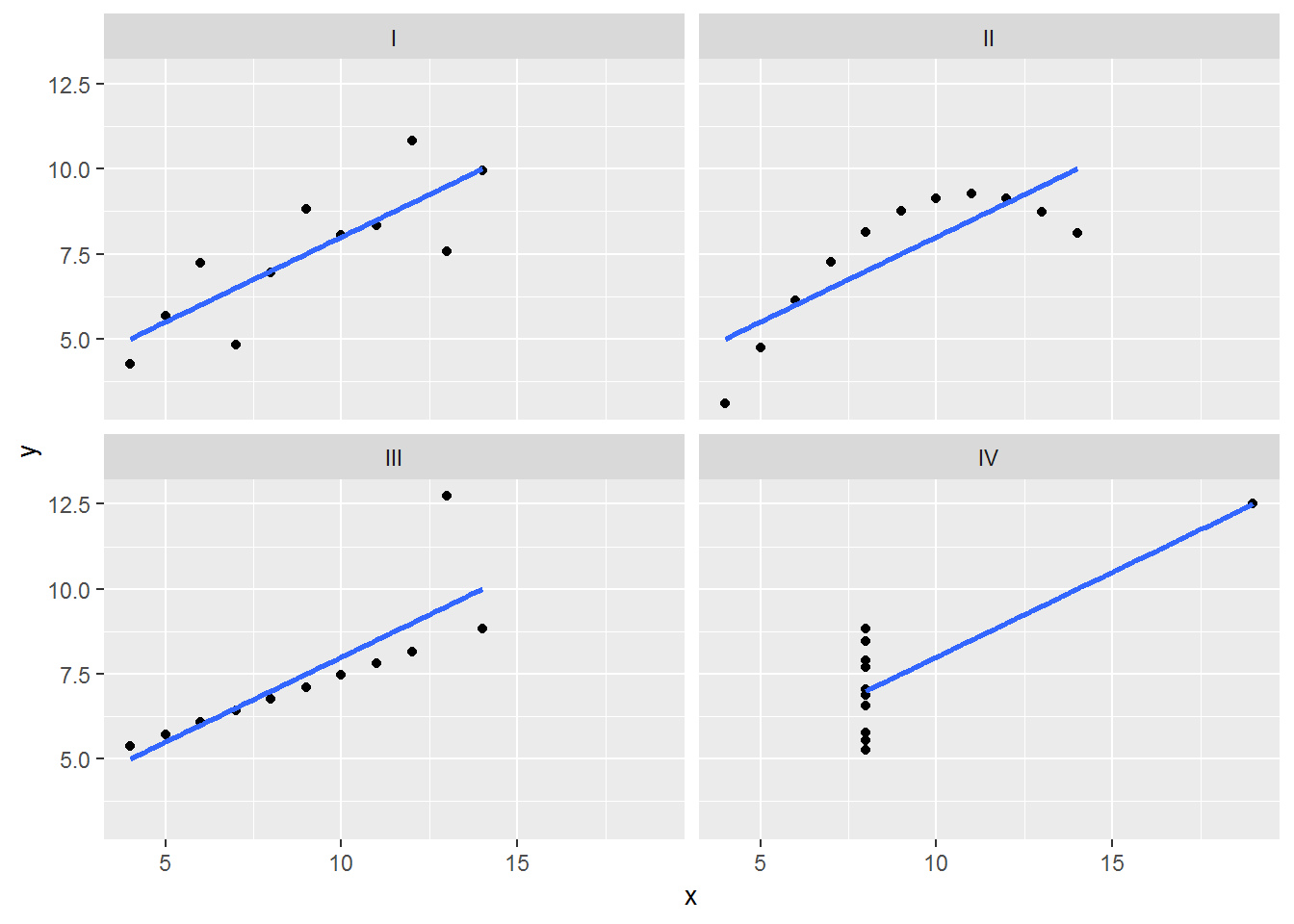
Figure 6.5: Les nuages de points et les droites de régression pour le quartet d’Anscombe.
6.4.2 DatasauRus
Les données disponibles dans la librairie datasauRus nous montrent pourquoi la visualisation est importante. Les treize ensembles de données possèdent tous les mêmes statiistiques descriptives et les mêmes droites de régression, mais leur aspect graphique est fort différent.
La table 6.2 montre les mesures pour les treize ensembles de données.
| dataset | moyenne des \(x\) | variance des \(x\) | moyenne des \(y\) | variance des \(y\) | coeff. de corrélation |
|---|---|---|---|---|---|
| away | 54.26610 | 281.2270 | 47.83472 | 725.7498 | -0.0641284 |
| bullseye | 54.26873 | 281.2074 | 47.83082 | 725.5334 | -0.0685864 |
| circle | 54.26732 | 280.8980 | 47.83772 | 725.2268 | -0.0683434 |
| dino | 54.26327 | 281.0700 | 47.83225 | 725.5160 | -0.0644719 |
| dots | 54.26030 | 281.1570 | 47.83983 | 725.2352 | -0.0603414 |
| h_lines | 54.26144 | 281.0953 | 47.83025 | 725.7569 | -0.0617148 |
| high_lines | 54.26881 | 281.1224 | 47.83545 | 725.7635 | -0.0685042 |
| slant_down | 54.26785 | 281.1242 | 47.83590 | 725.5537 | -0.0689797 |
| slant_up | 54.26588 | 281.1944 | 47.83150 | 725.6886 | -0.0686092 |
| star | 54.26734 | 281.1980 | 47.83955 | 725.2397 | -0.0629611 |
| v_lines | 54.26993 | 281.2315 | 47.83699 | 725.6388 | -0.0694456 |
| wide_lines | 54.26692 | 281.2329 | 47.83160 | 725.6506 | -0.0665752 |
| x_shape | 54.26015 | 281.2315 | 47.83972 | 725.2250 | -0.0655833 |
La figure 6.6 représente les 13 ensembles de données graphiquement avec leurs droites de régression.
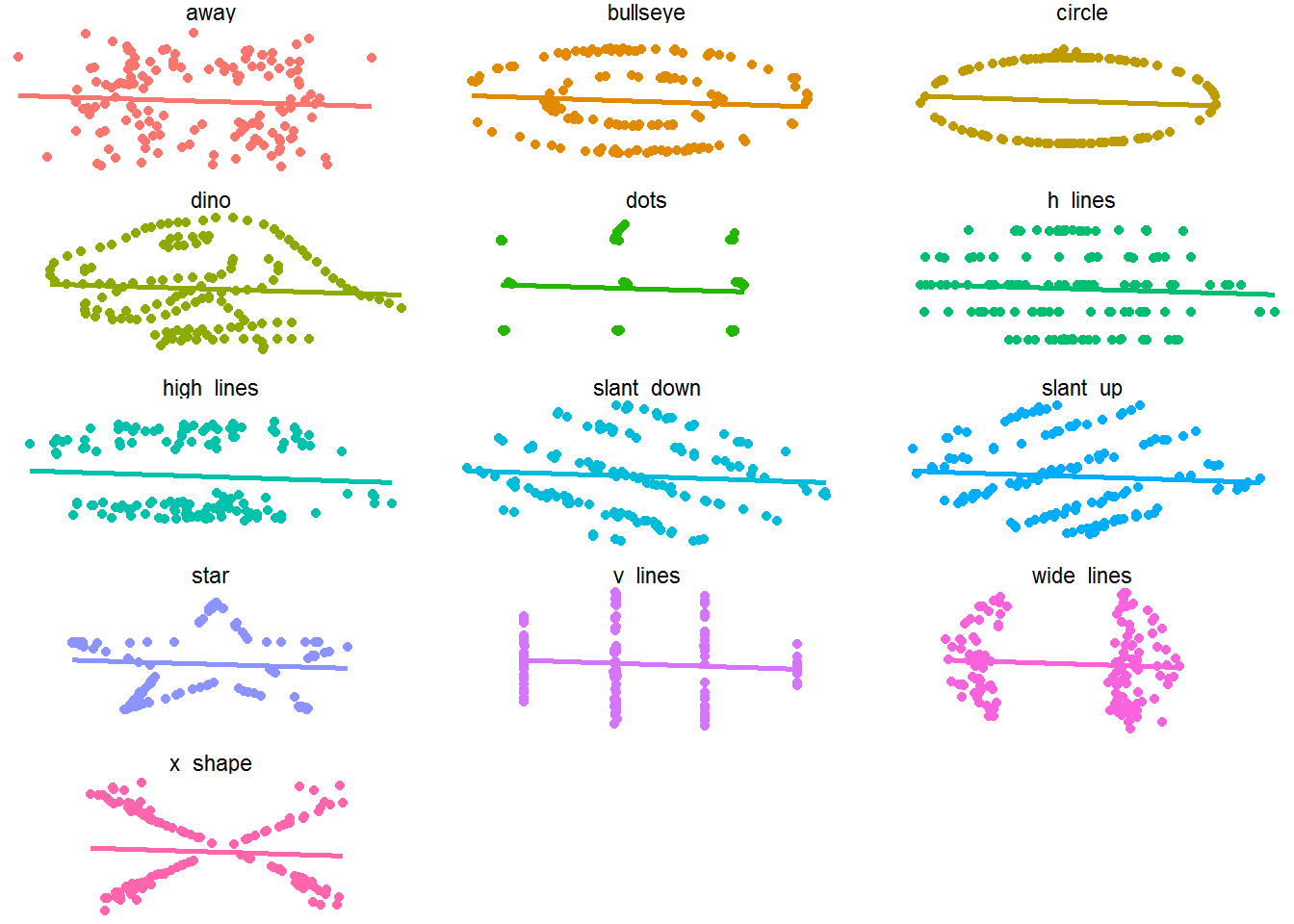
Figure 6.6: Les 13 ensembles de données de datasauRus.
6.4.3 D’autres types de régression
TODO… MAYBE