7.4 Le changement de coordonnées pour les intégrales doubles
Il existe d’autres systèmes de coordonnées autres que les systèmes cartésiens et polaires. En réalité, il est souvent impossible de résoudre certaines intégrales en n’utilisant que ces deux systèmes. Par exemple, si nous voulons calculer \(\iint\limits_D 1 dA\) sur le domaine \(D=\left\{(x,y)\in\mathbb{R}^2\left| \frac{x^2}{a^2}+\frac{y^2}{b^2}\leq 1 \right. \right\}\), il devient très difficile de faire cette intégrale en n’utilisant que les deux systèmes que nous connaissons. Heureusement, il existe une technique permettant de trouver le terme \(dA\) lorsque nous effectuons un changement de variables. Avant de débuter, nous ferons un bref rappel du produit vectoriel.
7.4.1 Le produit vectoriel
Soit deux vecteurs de \(\mathbb{R}^3\) non-colinéaires tels que \(\overrightarrow{u}=[u_1,u_2,0]\) et \(\overrightarrow{v}=[v_1,v_2,0]\). L’aire du parallélogramme engendré par ces vecteurs est donnée par: \[\begin{align*} A&= \| \vec u \times \vec v\| \\ &= \left\| \ \left| \begin{array}{ccc} \vec i &\vec j& \vec k\\ u_1 & u_2 &0 \\ v_1 & v_2 &0 \end{array} \right|\ \right\| \\ &=\left\| 0\vec i - 0\vec j+\left| \begin{array}{cc} u_1 & u_2 \\ v_1 & v_2 \end{array} \right|\vec k \ \right\| \\ &= \left| det \left(\begin{array}{cc} u_1 & u_2 \\ v_1 & v_2 \end{array} \right) \right| \end{align*}\] L’aire du prallélogramme est donc donnée par la valeur absolue du déterminant des deux vecteurs.
7.4.2 Le changement de coordonnées
Nous voulons déterminer une expression dans un autre système de coordonnées (par exemple \(u\) et \(v\)) pour \(\iint\limits_D f(x,y)dA\). Plus précisément, nous voulons trouver une expression pour \(dA\) en fonction de \(u\) et \(v\). Pour ce faire, supposons qu’il existe une transformation bijective et dérivable \(T\) qui prend une région \(D'\) du plan \(uv\) et qui l’envoie sur \(D\) dans le plan \(xy\). Ceci signifie que \(T\) prend un point \((u,v)\in D'\) et l’envoie sur le point \((x(u,v),y(u,v))\in D\). La figure 7.9 représente cette transformation.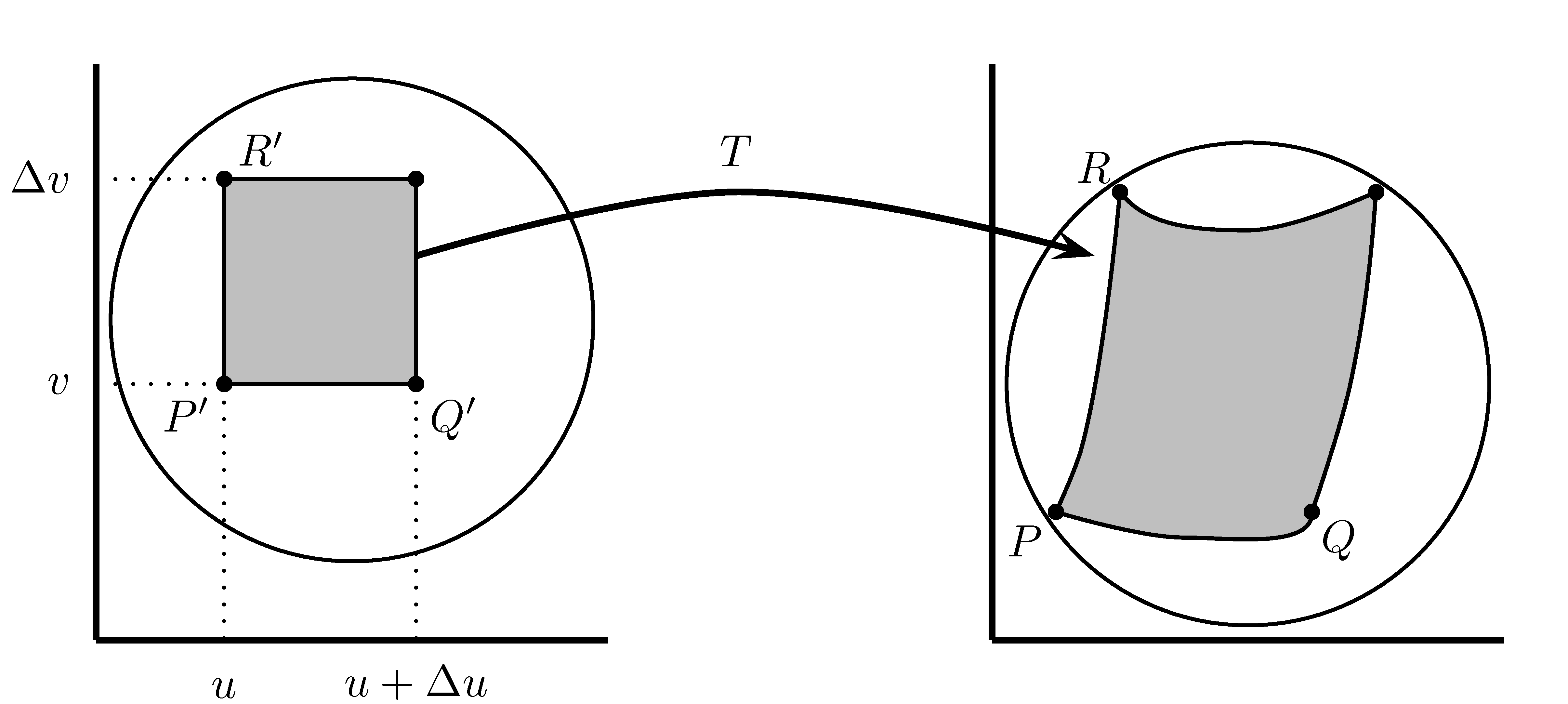
Figure 7.9: La représentation de l’effet de la transformation \(T\) sur un rectangle dans le plan \(x\) et \(y\).
Nous allons étudier le résultat de cette transformation sur un petit rectangle de dimension \(\Delta u \times \Delta v\) dans le plan \(uv\). Notons par \(P=T(P')\), \(Q=T(Q')\) et \(R=T(R')\). On sait qu’une petite variation \(\Delta x\) peut être obtenue par \[\begin{align*} \Delta x\approx \frac{\partial x}{\partial u}\Delta u+\frac{\partial x}{\partial v}\Delta v \end{align*}\] De même, on a \[\begin{align*} \Delta y\approx \frac{\partial y}{\partial u}\Delta u+\frac{\partial y}{\partial v}\Delta v \end{align*}\] Ainsi, le vecteur \(\overrightarrow{PQ}=\left[\frac{\partial x}{\partial u}\Delta u,\frac{\partial y}{\partial u}\Delta u\right]\), car \(\Delta v=0\) puisque les points \(P'\) et \(Q'\)ont la même composante \(v\). De même, on a que le vecteur \\(\overrightarrow{PR}=\left[\frac{\partial x}{\partial v}\Delta v,\frac{\partial y}{\partial v}\Delta v\right]\) pour des raisons similaires. Maintenant, l’élément d’aire \(\Delta A\) formé par \(\Delta u\) et \(\Delta v\) s’exprime en terme d’aire de parallélogramme \[\begin{align*} \Delta A&\approx \left\| \overrightarrow{PQ}\times \overrightarrow{PR}\right\| \\ &\approx \left\| \left| \begin{array}{ccc} \vec i &\vec j& \vec k\\ \frac{\partial x}{\partial u}\Delta u & \frac{\partial y}{\partial u}\Delta u &0 \\ \frac{\partial x}{\partial v}\Delta v & \frac{\partial y}{\partial v}\Delta v &0 \end{array} \right| \right\|\\ &\approx \left\| 0\vec i -0\vec j+ \left| \begin{array}{cc} \frac{\partial x}{\partial u}\Delta u & \frac{\partial y}{\partial u}\Delta u \\ \frac{\partial x}{\partial v}\Delta v & \frac{\partial y}{\partial v}\Delta v \end{array} \right| \vec k \right\|\\ &\approx \sqrt{\left(\frac{\partial x}{\partial u}\Delta u \frac{\partial y}{\partial v}\Delta v- \frac{\partial y}{\partial u}\Delta u \frac{\partial x}{\partial v}\Delta v\right)^2}\\ &\approx \left|\frac{\partial x}{\partial u}\frac{\partial y}{\partial v}- \frac{\partial y}{\partial u} \frac{\partial x}{\partial v}\right|\Delta u\Delta v.\\ \end{align*}\] À la limite où \(\Delta u\) et \(\Delta v\) tendent vers \(0\), nous obtenons une expression pour \(dA\): \[\begin{align*} dA=\left|\frac{\partial x}{\partial u}\frac{\partial y}{\partial v}- \frac{\partial y}{\partial u} \frac{\partial x}{\partial v}\right|dudv \end{align*}\]
Définition 7.4 (Jacobien) Soit une transformation dérivable \(T:(u,v)\rightarrow (x(u,v),y(u,v))\). Nous appelons Jacobien le déterminant suivant: \[\begin{align*} J&=\left|\begin{array}{cc} \frac{\partial x}{\partial u} & \frac{\partial x}{\partial v} \\ \frac{\partial y}{\partial u} & \frac{\partial y}{\partial v} \end{array} \right| =\frac{\partial x}{\partial u}\frac{\partial y}{\partial v}- \frac{\partial y}{\partial u} \frac{\partial x}{\partial v} \end{align*}\]
Nous pouvons donc écrire \(dA=|J|dudv\), d’où: \[\iint\limits_D f(x,y)dA=\iint\limits_{D'} f(x(u,v),y(u,v))|J|dudv\]
Exemple 7.23 Calculez \(\iint\limits_D (x^2-xy+y^2)dA\) où \(D\) est l’ellipse donnée par \(x^2-xy+y^2=2\) en utilisant la transformation: \[\begin{align*} x &= \sqrt{2}u-\sqrt{2/3}v \\ y &= \sqrt{2}u+\sqrt{2/3}v \end{align*}\]