2.4 Les équations différentielles à coefficients constants d’ordre 2
2.4.1 Quelques rappels concernant les nombres complexes
Définition 2.8 (Nombre complexe) Un nombre complexe \(z\) s’écrit sous la forme \(z=a+bi\), où \(a,b \in \mathbb{R}\) et tel que \(i^2=-1\).
Nous disons que \(a\) est la partie réelle de \(z\) et \(b\) est la partie imaginaire de \(z\).
L’ensemble des nombres complexes est noté \(\mathbb{C}\).
Nous pouvons également écrire \(z\) sous une form dite polaire qui est \(z=r(\cos(\theta)+i\sin(\theta))\), où \(r=\sqrt{a^2+b^2}\) et \(\theta=\text{Arctan}\left(\dfrac{b}{a}\right)\).La figure 2.1 permet de représenter un nombre complexe de façon géométrique.
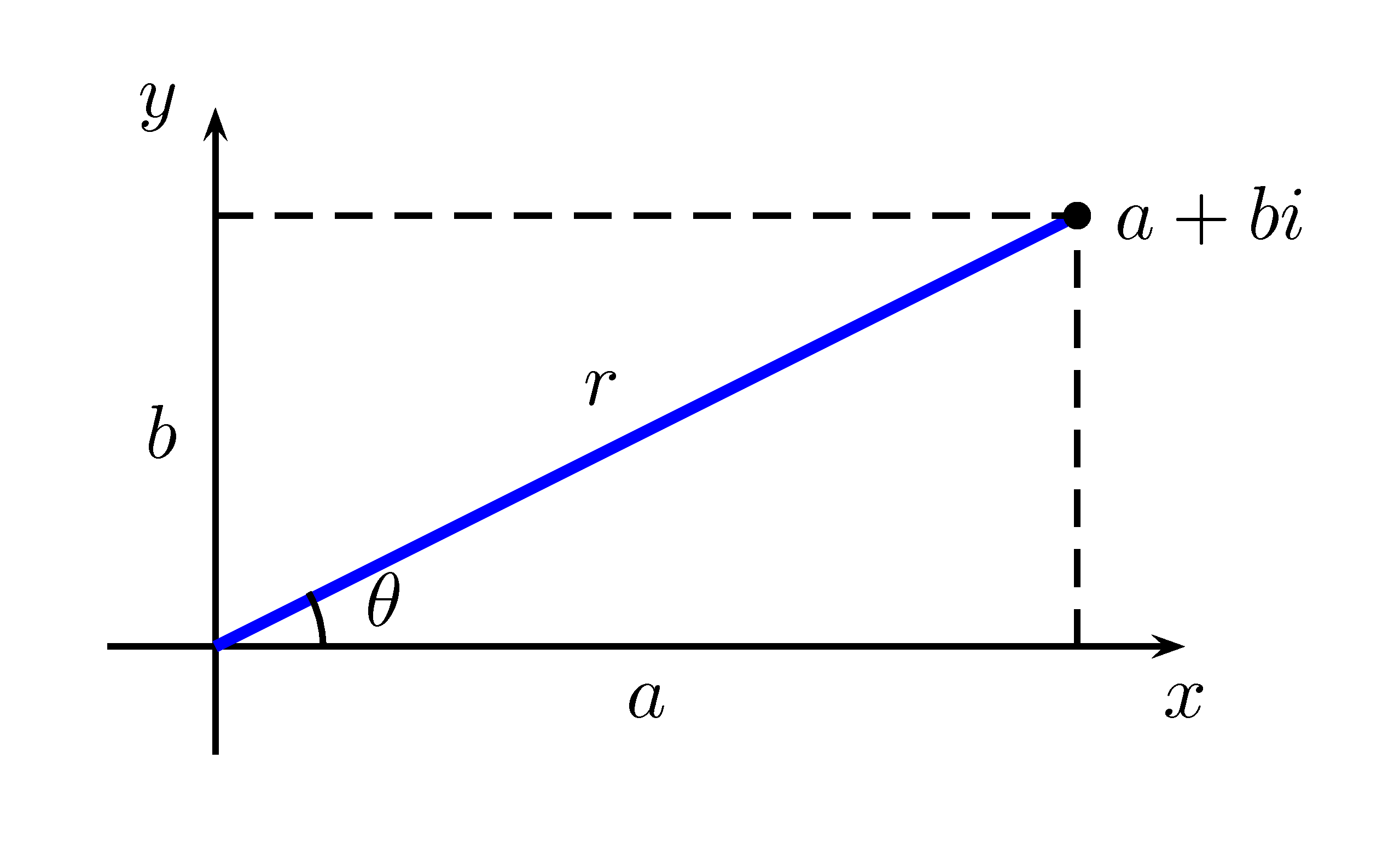
Figure 2.1: Représentation d’un nombre complexe
Corollaire 2.1 Nous avons: \[\begin{align*} \cos(\theta) &= \dfrac{e^{i\theta}+e^{-i\theta}}{2} \\ \sin(\theta) &= \dfrac{e^{i\theta}-e^{-i\theta}}{2i} \end{align*}\]
Preuve. Pour démontrer ce résultat, nous utiliserons le théorème 2.1. Nous avons: \[\begin{align} e^{i\theta} &= \cos(\theta)+i\sin(\theta)\tag{2.1} \\ e^{-i\theta} &= \cos(-\theta)+i\sin(-\theta) \notag \\ &= \cos(\theta)-i\sin(\theta)\tag{2.2} \end{align}\]
Si nous additions les équations (2.1) et (2.2): \[\begin{align*} e^{i\theta}+e^{-i\theta} &= \cos(\theta)+i\sin(\theta)+\cos(\theta)-i\sin(\theta) \\ &= 2\cos(\theta) \\ \cos(\theta) &= \dfrac{e^{i\theta}+e^{-i\theta}}{2} \end{align*}\]
Si nous faisons la différence entre les équations (2.1) et (2.2): \[\begin{align*} e^{i\theta}-e^{-i\theta} &= \cos(\theta)+i\sin(\theta)-(\cos(\theta)-i\sin(\theta)) \\ &= 2i\sin(\theta) \\ \sin(\theta) &= \dfrac{e^{i\theta}-e^{-i\theta}}{2i} \end{align*}\]
2.4.2 Les équations différentielles homogènes à coefficients constants d’ordre 2
Le terme homogène indique que le membre de droite de l’équation (2.3) est nul. Nous traiterons le cas à la section 2.4.3.
Avant de résoudre ce type d’équations différentielles, la prochaine proposition sera cruciale.
Preuve. Nous avons que: \[\begin{align*} ay_1''+by_1'+cy_1 &= 0 \\ ay_2''+by_2'+cy_2 &= 0 \end{align*}\] car \(y_1\) et \(y_2\) sont des solutions de (2.3). Nous avons que: \[\begin{align*} y &= C_1y_1+C_2y_2 \\ y' &= C_1y_1'+C_2y_2' \\ y'' &= C_1y_1''+C_2y_2'' \\ \end{align*}\] Ainsi: \[\begin{align*} ay''+by'+cy &= a(C_1y_1''+C_2y_2'')+b(C_1y_1'+C_2y_2')+c(C_1y_1+C_2y_2) \\ &= C_1\underbrace{(ay_1''+by_1'+cy_1)}_{=\ 0}+C_2\underbrace{(ay_2''+by_2'+cy_2)}_{=\ 0} \\ &= 0 \end{align*}\]
Une combinaison linéaire de solutions est aussi une solution.
Nous pouvons maintenant résoudre l’équation (2.3) en supposant que la solution est de la forme \(y=e^{rx}\), où \(r\) est une constante qu’il nous reste à déterminer.
Pour résoudre une équation différentielle homogène d’ordre 2 à coefficients constants, il faut toujours poser la solution \(y=e^{rx}\).
Nous avons donc: \[\begin{align*} y &= e^{rx} \\ y' &= re^{rx} \\ y'' &= r^2e^{rx} \end{align*}\]
Nous substituons ces résultats dans l’équation (2.3): \[\begin{align} a\dfrac{d^2y}{dx^2}+b\dfrac{dy}{dx}+cy &= 0 \notag \\ ar^2e^{rx}+bre^{rx}+ce^{rx} &= 0 \notag \\ e^{rx}(ar^2+br+c) &= 0 \notag \\ ar^2+br+c &= 0\tag{2.4} \end{align}\]
L’équation (2.4) se nomme polynôme caractéristique de l’équation (2.3). Déterminer les valeurs de \(r\) revient à trouver les racines du polynôme caractéristique et donc: \[\begin{align*} r_{1,2} &= \dfrac{-b\pm\sqrt{b^2-4ac}}{2a} \end{align*}\] Nous devrons étudier trois cas distincts qui dépendent du discriminant \(b^2-4ac\).
2.4.2.1 Cas 1: \(b^2-4ac>0\)
Dans ce cas, le polynôme caractéristique fournit deux valeurs de \(r\) réelles, que nous notons \(r_1\) et \(r_2\). Nous avons donc \(y_1(x)=e^{r_1x}\) qui est une solution de (2.3) et également \(y_2=e^{r_2x}\). Par la proposition 2.1, nous obtenons la solution générale: \[\begin{align*} y(x) &= C_1e^{r_1x}+C_2e^{r_2x} \end{align*}\] où \(C_1,C_2\in\mathbb{R}\).
2.4.2.2 Cas 2: \(b^2-4ac<0\)
Dans ce cas, le polynôme caractéristique fournit deux valeurs de \(r\) complexes. Posons \(\gamma=-\dfrac{b}{2a}\) et \(\omega=\dfrac{\sqrt{4ac-b^2}}{2a}\) ce qui implique que \(r_1=\gamma+\omega i\) et \(r_2=\gamma -\omega i\). Nous avons donc deux solutions à l’équation (2.3), soit \(y_1=e^{r_1x}=e^{(\gamma+\omega i)x}\) et \(y_2=e^{r_2x}=e^{(\gamma-\omega i)x}\).
Puisque les solutions précédentes sont complexes, nous allons utiliser la proposition 2.1 et le corollaire 2.1 pour créer deux nouvelles solutions réelles: \[\begin{align*} y_3(x) &= \dfrac{y_1(x)+y_2(x)}{2} \\ &= \dfrac{e^{(\gamma+\omega i)x}+e^{(\gamma-\omega i)x}}{2} \\ &= e^{\gamma x}\left( \dfrac{e^{\omega i x}+e^{-\omega i x}}{2} \right) \\ &= e^{\gamma x}\cos(\omega x) \\ y_4(x) &= \dfrac{y_1(x)-y_2(x)}{2i} \\ &= \dfrac{e^{(\gamma+\omega i)x}-e^{(\gamma-\omega i)x}}{2i} \\ &= e^{\gamma x}\left( \dfrac{e^{\omega i x}-e^{-\omega i x}}{2i} \right) \\ &= e^{\gamma x}\sin(\omega x) \end{align*}\]
D’où la solution générale de l’équation (2.3) est: \[\begin{align*} y(x) &= e^{\gamma x}\left( C_1\cos(\omega x)+C_2\sin(\omega x) \right) \end{align*}\]
2.4.2.3 Cas 3: \(b^2-4ac=0\)
Dans ce cas, nous n’obtenons qu’une seule valeur de \(r=-\dfrac{b}{2a}\). Puisque nous n’avons qu’une seule solution, nous devons en trouver une autre pour être en mesure de construire une combinaison linéaire. Nous allons démontrer que \(y_2(x)=xe^{rx}\) est aussi une solution de l’équation différentielle (2.3).Preuve. \[\begin{align*} y_2 &= xe^{rx} \\ y_2' &= e^{rx}+rxe^{rx} \\ y_2'' &= re^{rx}+re^{rx}+r^2xe^{rx} \end{align*}\] Et donc: \[\begin{align*} ay'' +by' +cy &= 0 \\ a(2re^{rx}+r^2xe^{rx})+b(e^{rx}+rxe^{rx})+c(xe^{rx}) &= 0 \\ e^{rx}(2ar+ar^2x+b+brx+cx) &= 0 \\ e^{rx}(\underbrace{(ar^2+br+c)}_{=0}x+\underbrace{(2ar+b)}_{=0}) &= 0 \end{align*}\]
La solution générale est donc de la forme: \[\begin{align*} y(x) &= C_1e^{rx}+C_2xe^{rx} \end{align*}\]
Exemple 2.26 Trouvez les solutions des équations différentielles suivantes:
- \(y''-9y'+20y=0\)
- \(2y''-4y'+8y=0\)
- \(y''+6y'+9=0\)
2.4.3 Les équations différentielles non homogènes à coefficients constants d’ordre 2
Pour résoudre ce type d’équations différentielles, nous aurons besoin du théorème suivant:
Théorème 2.2 Soit une équation différentielle de la forme: \[\begin{align*} a\dfrac{d^2y}{dx^2}+b\dfrac{dy}{dx}+cy &= F(x) \end{align*}\] La solution de cette équation différentielle est de la forme: \[\begin{align*} y(x) &= C_1y_1(x)+C_2y_2(x)+y_p \end{align*}\] où \(y_1\) et \(y_2\) sont les solutions de l’équation homogène associée à l’équation (2.5), c’est-à-dire: \[\begin{align*} a\dfrac{d^2y}{dx^2}+b\dfrac{dy}{dx}+cy &= 0 \end{align*}\] et \(y_p\) est une solution particulière de l’équation non homogène.
Nous verrons deux méthodes pour trouver \(y_p\).
2.4.3.1 La méthode des coefficients indéterminés
Cette méthode consiste à étudier la nature de la fonction \(F(x)\) et à supposer que \(y_p\) est de même nature. La table 2.1 montre la forme de la solution particulière \(y_p\) selon la nature de \(F(x)\).
| Forme de \(F(x)\) | Forme de \(y_p\) |
|---|---|
| Polynôme de degré \(n\) | \(y_p=a_nx^n+a_{n-1}x^{n-1}+\ldots+a_x+a_0\) |
| \(F(x)\) possède un \(\sin(\omega x)\) et/ou un \(\cos(\omega x)\) | \(y_p=A\cos(\omega x)+B\sin(\omega x)\) |
| \(F(x)\) possède une exponentielle \(e^{\alpha x}\) | \(y_p=A^{\alpha x}\) |
2.4.3.2 La méthode de variation des paramètres (ou méthode de Lagrange)
La méthode de variation des paramètres est souvent plus longue à utiliser que la méthode des coefficients indéterminés, par contre, elle est valide pour tous les types de fonctions \(F(x)\).
Nous débutons en trouvant les solutions \(y_1\) et \(y_2\) de l’équation différentielle homogène associée à l’équation: \[\begin{align*} ay''+by'+cy=F(x) \end{align*}\]
Supposons que la solution est de la forme : \[\begin{align*} y(x) &= \mu_1(x)y_1(x)+\mu_2(x)y_2(x) \end{align*}\] Afin d’alléger la notation, nous omettrons la dépendance en \(x\). Nous cherchons donc \(\mu_1\) et \(\mu_2\). Avant de substituer dans l’équation différentielle, nous allons trouver les dérivées successives de \(y\). \[\begin{align*} y' &= \mu_1y_1'+\mu_1'y_1+\mu_2'y_2+\mu_2y_2' \end{align*}\] Nous allons maintenant faire la supposition que \(\mu_1'y_1+\mu_2'y_2=0\) et donc: \[\begin{align*} y' &= \mu_1y_1'+\mu_2y_2' \end{align*}\] Trouvons maintenant la dérivée seconde: \[\begin{align*} y' &= \mu_1'y_1'+\mu_1y_1''+\mu_2'y_2'+\mu_2y_2'' \end{align*}\] Nous avons donc: \[\begin{align*} ay''+by'+cy &= F(x) \\ a(\mu_1'y_1'+\mu_1y_1''+\mu_2'y_2'+\mu_2y_2'')+b(\mu_1y_1'+\mu_2y_2')+c(\mu_1y_1+\mu_2y_2) &= F(x) \\ \mu_1\underbrace{(ay_1''+by_1'+cy_1)}_{=0}+\mu_2\underbrace{(ay_2''+by_2'+cy_2)}_{=0}+\mu_1'y_1'+\mu_2'y_2' &= F(x) \\ \mu_1'y_1'+\mu_2'y_2' &= F(x) \end{align*}\] Ainsi, pour déterminer \(\mu_1\) et \(\mu_2\), nous avons les deux équations suivantes: \[\begin{align*} \mu_1'y_1+\mu_2'y_2 &= 0 \\ \mu_1'y_1'+\mu_2'y_2' &= F(x) \end{align*}\] Nous pouvons utiliser la méthode de Cramer pour résoudre ce système d’équations linéaires: \[\begin{align*} \mu_1'&= \dfrac{ \begin{vmatrix} 0&y_2\\ F(x)&y_2' \end{vmatrix}}{ \begin{vmatrix} y_1 &y_2\\ y_1'&y_2' \end{vmatrix} }=-\dfrac{y_2F(x)}{W(y_1,y_2)}\\ \mu_2'&= \dfrac{ \begin{vmatrix} y_1&0\\ y_1'&F(x) \end{vmatrix}}{ \begin{vmatrix} y_1 &y_2\\ y_1'&y_2' \end{vmatrix} }=\dfrac{y_1F(x)}{W(y_1,y_2)} \end{align*}\]
Définition 2.11 (Wronskien) Nous appelons le Wronskien de deux fonctions \(y_1\) et \(y_2\), le résultat suivant: \[\begin{align*} W(y_1,y_2)=\begin{vmatrix} y_1 &y_2\\ y_1'&y_2' \end{vmatrix} \end{align*}\]
Nous pouvons maintenant trouver nos deux fonctions \(\mu_1\) et \(\mu_2\): \[\begin{align*} \mu_1&=-\int \dfrac{y_2(x)F(x)}{W(y_1,y_2)}dx\\ \mu_2&=\int \dfrac{y_1(x)F(x)}{W(y_1,y_2)}dx \end{align*}\]
Exemple 2.31 Trouvez les solutions des équations différentielles suivantes en utilisant les deux méthodes:
- Méthode des coefficients indéterminés
- Méthode de variation des paramètres
- \(y''-2y'+y=2x\)
- \(y''-y'-6y=e^{-x}\)