6.7 Les multiplicateurs de Lagrange
La méthode des multiplicateurs de Lagrange permet de maximiser ou de minimiser une fonction générale \(f(x,y,z)\) sujette à une contrainte de la forme \(g(x,y,z)=k\).
Il est plus simple d’expliquer la méthode de Lagrange d’un point de vue géométrique pour des fonctions de deux variables. Nous commençerons donc par essayer de trouver les valeurs extrèmes d’une fonction \(f(x,y)\) soumise à une contrainte de la forme \(g(x,y)=k\). Nous sommes donc à la recherche des valeurs extrèmes par lesquelles passerait la fonction \(f(x,y)\) lorsque le point \((x,y)\) doit se trouver sur la courbe de niveau \(g(x,y)=k\). La figure 6.8 montre cette courbe ainsi que plusieurs courbe de niveau de \(f(x,y)\), c’est-à-dire \(f(x,y)=c\).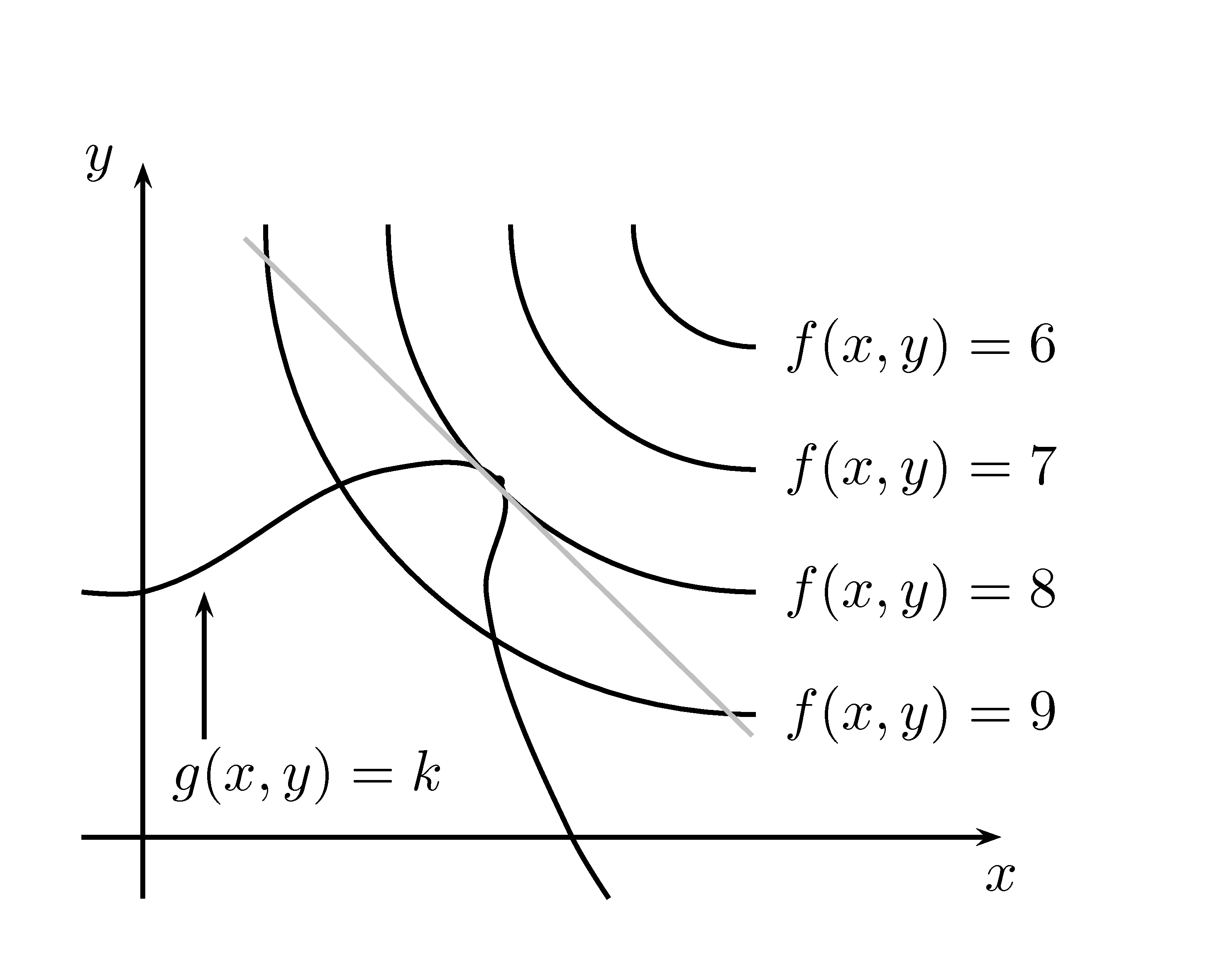
Figure 6.8: Représentation géométrique de la méthode des multiplicateurs de Lagrange.
Maximiser (ou minimiser) \(f(x,y)\) sous la contrainte \(g(x,y)=k\) revient à trouver la plus grande (petite) valeur de \(c\) telle que la courbe de niveau \(f(x,y)=c\) coupe \(g(x,y)=k\). En observant la figure 6.8, il est clair que cela se produit lorsque ces courbes ont une tangente en commun. Donc, en un point \((x_0,y_0)\) où les courbes se touchent, elles ont la même droite normale. Les vecteurs gradients sont donc parallèles, ce qui s’écrit \(\nabla f(x_0,y_0)=\lambda \nabla g(x_0,y_0)\) pour un certain scalaire \(\lambda\).
Ce type d’argumentation s’applique également au problème de trouver les valeurs extrèmes de \(f(x,y,z)\) soumise à une contrainte \(g(x,y,z)=k\).
La méthode des multiplicateurs de Lagrange peut donc être décrite de la façon suivante. Pour déterminer les valeurs extrèmes (maximales ou minimales) de \(f(x,y,z)\) soumises à la contrainte \(g(x,y,z)=k\):
Cherchez toutes les valeurs de \(x\), \(y\), \(z\) et \(\lambda\) telles que \(\nabla f(x,y,z) = \lambda \nabla g(x,y,z)\) et \(g(x,y,z)=k\).
Calculez la valeur de \(f\) en tous les points \((x,y,z)\) trouvés à l’étape 1. La plus grande de ces valeurs est le maximum de \(f\); la plus petite de ces valeurs est le minimum de \(f\).